(1,5 điểm) Biểu đồ cột kép ở hình bên dưới biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 của nước ta.

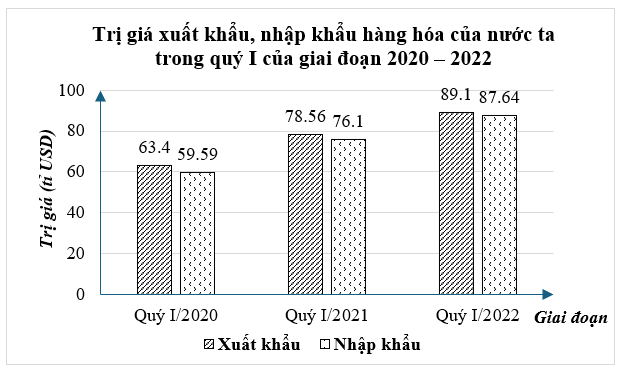
(Nguồn: Tổng cục Hải quan)

a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 (đơn vị: tỷ USD) theo mẫu sau:

b) Giá trị xuất khẩu hàng hóa của nước ta trong quý I năm 2021 tăng hay giảm bao nhiêu phần trăm so với quý I năm 2020 (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

Đáp án:

a) Sai.

b) Đúng.

c) Đúng.

d) Sai.

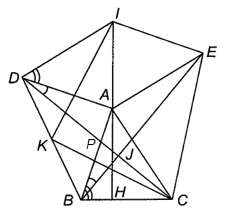
⦁ Giả sử \[AI\] cắt \[BC\] ở \[H\].

Ta có: \[\widehat {DAI} + \widehat {DAB} + \widehat {BAH} = 180^\circ \], mà \[\widehat {DAB} = 90^\circ \] (do \[\Delta DAB\] vuông cân tại \[A\]).

Suy ra \[\widehat {DAI} + \widehat {BAH} = 90^\circ \]. Do đó ý a) sai.

⦁ Ta có \[\widehat {DAI} = \widehat {ABC}\] (gt) nên \[\widehat {ABH} + \widehat {BAH} = 90^\circ \].

Trong \[\Delta ABH\] có: \[\widehat {ABH} + \widehat {BAH} + \widehat {AHB} = 180^\circ \].

Suy ra \[\widehat {AHB} = 180^\circ \left( {\widehat {ABH} + \widehat {BAH}} \right) = 180^\circ - 90^\circ = 90^\circ \] hay \[AI \bot BC\]. Do đó ý b) đúng.

⦁ Ta có \[\widehat {BAE} = \widehat {BAC} + \widehat {CAE} = \widehat {BAC} + 90^\circ \] và \[\widehat {DAC} = \widehat {BAC} + \widehat {BAD} = \widehat {BAC} + 90^\circ \].

Do đó \[\widehat {BAE} = \widehat {DAC}\].

Xét \[\Delta BAE\] và \[\Delta DAC\] có:

\[AB = AD;\,\,\widehat {BAE} = \widehat {DAC};\,\,AC = AE\];

Do đó \[\Delta BAE = \Delta DAC\] (c.g.c).

Suy ra \(\widehat {EBA} = \widehat {CDA}\) (hai góc tương ứng). Do đó ý c) đúng.

⦁ Tam giác \[ABD\] vuông cân tại \[A\] nên \[AK\] vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó \(\widehat {DAK} = \frac{1}{2}\widehat {BAD} = 45^\circ \).

Khi đó \(\widehat {ABK} = \widehat {BAK} = 45^\circ \) nên \[\Delta ABK\] vuông cân tại \[K\], do đó \[KA = KB\]. Do đó ý d) sai.

Hướng dẫn giải

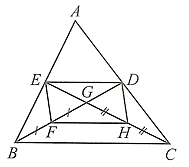
a) Tam giác \[ABC\] có các đường trung tuyến \[BD,{\rm{ }}CE\] cắt nhau tại \[G\] nên \[G\] là trọng tâm \[\Delta ABC,\] do đó \(DG = \frac{1}{2}BG,\) \(EG = \frac{1}{2}CG.\)

Mà \[F,{\rm{ }}H\] lần lượt là trung điểm của \[BG,{\rm{ }}CG\] nên

\(BF = FG = \frac{1}{2}BG,\) \(CH = HG = \frac{1}{2}CG.\)

Do đó \[DG = BF = FG,{\rm{ }}EG = CH = HG.\]

Suy ra, \[G\] là trung điểm của \[FD,{\rm{ }}G\] là trung điểm của \[EH.\]

Tứ giác \[EFHD\] có hai đường chéo \[EH\] và \(FD\) cắt nhau tại trung điểm \[G\] của mỗi đường nên \[EFHD\] là hình bình hành.

b) Để hình bình hành \[EFHD\] là hình vuông thì \[EH = DF\] và \[EH \bot DF.\]

Suy ra \[EG = DG,{\rm{ }}BG = CG\] và \[BD \bot CE.\]

⦁ Xét \(\Delta BEG\) và \[\Delta CDG\] có:

\[BG = CG,\] \(\widehat {EGB} = \widehat {DGC}\) (đối đỉnh), \[EG = DG\]

Do đó \(\Delta BEG = \Delta CDG\) (c.g.c).

Suy ra \[BE = CD\] (hai cạnh tương ứng).\[\left( 1 \right)\]

Mà \[BD,{\rm{ }}CE\] là các đường trung tuyến của \(\Delta ABC\) nên \[E\] là trung điểm của \[AB,{\rm{ }}D\] là trung điểm của \[AC.\]

Suy ra \[AB = 2BE,{\rm{ }}AC = 2CD.\,\,\,\,\,\,\left( 2 \right)\]

Từ (1) và (2) suy ra \[AB = AC.\]

⦁ Dễ thấy, nếu \[AB = AC\] và \[BD \bot CE\] thì tứ giác \[EFHD\] là hình vuông.

Vậy tam giác \[ABC\] cân tại \[A\] có hai đường trung tuyến \[BD,CE\] vuông góc với nhau thì tứ giác \[EFHD\] là hình vuông.