Cho đa thức \(U = \left( {10{x^5}{y^3} - 25{x^3}{y^2} + 20{x^4}{y^3}} \right):\left( { - 5{x^2}{y^2}} \right)\) và \(V = 2{x^2}y\left( {x + 2} \right)\).
a) Hệ số cao nhất của của đa thức \(U\) là 5.
b) Giá trị của biểu thức \(U\) tại \(x = - 1\,;\,\,y = 2\) là 10.
c) Bậc của đa thức \(V\) là 4.
d) Tổng của hai đa thức \(U\) và \(V\) chia hết cho 5.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án:
a) Sai.
b) Sai.
c) Đúng.
d) Đúng.
⦁ Ta có \(U = \left( {10{x^5}{y^3} - 25{x^3}{y^2} + 20{x^4}{y^3}} \right):\left( { - 5{x^2}{y^2}} \right)\)
\[ = 10{x^5}{y^3}:\left( { - 5{x^2}{y^2}} \right) - 25{x^3}{y^2}:\left( { - 5{x^2}{y^2}} \right) + 20{x^4}{y^3}:\left( { - 5{x^2}{y^2}} \right)\]
\[ = - 2{x^3}y + 5x - 4{x^2}y\].
Khi đó, hệ số cao nhất của của đa thức \(U\) là \[ - 2\]. Do đó ý a) sai.
⦁ Thay \(x = - 1\,;\,\,y = 2\) vào biểu thức \(U\), ta có:
\(U = 2 \cdot {\left( { - 1} \right)^3} \cdot 2 + 5 \cdot \left( { - 1} \right) - 4 \cdot {\left( { - 1} \right)^2} \cdot 2 = - 4 - 5 - 8 = - 10.\)
Như vậy với \(x = - 1\,;\,\,y = 2\) thì \(U = - 10\). Do đó ý b) sai.
⦁ Ta có \(V = 2{x^2}y\left( {x + 2} \right)\)\( = 2{x^2}y \cdot x + 2{x^2}y \cdot 2\)\( = 2{x^3}y + 4{x^2}y\).
Khi đó, bậc của đa thức \(V\) là 4. Do đó ý c) đúng.
⦁ Ta có \[U + V = \left( { - 2{x^3}y + 5x - 4{x^2}y} \right) + \left( {2{x^3}y + 4{x^2}y} \right)\]
\[ = \left( { - 2{x^3}y + 2{x^3}y} \right) + 5x + \left( { - 4{x^2}y + 4{x^2}y} \right) = 5x.\]
\[ = \left( { - 2{x^3}y + 2{x^3}y} \right) + 5x + \left( { - 4{x^2}y + 4{x^2}y} \right) = 5x\].
Vì \[5x\,\, \vdots \,\,5\] nên \(\left( {U + V} \right)\,\, \vdots \,\,5\).
Như vậy, tổng của hai đa thức \(U\) và \(V\) chia hết cho 5. Do đó ý d) đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Một kho chứa có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 6 m và trung đoạn là \[3{\rm{ m}}.\] Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ p (ảnh 1)](https://video.vietjack.com/upload2/images/1752817036/1752817098-image6.png)
Lời giải
Hướng dẫn giải
Đáp số: \[{\bf{1}},{\bf{45}}\].
Nửa chu vi đáy của kho chứa là: \[\left( {6 \cdot \;4} \right):2 = 12\,\,\left( {\rm{m}} \right).\]
Diện tích xung quanh của kho chứa là: \[12 \cdot 3 = 36{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\]
Diện tích cần sơn phủ là: \[36 - 7 = 29{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\]
Số tiền cần trả để hoàn thành việc sơn phủ là:
\[29 \cdot 50{\rm{ }}000 = 1\,\,450\,\,000\] (đồng) \[ = 1,45\] (triệu đồng).
Vậy số tiền cần trả để hoàn thành việc sơn phủ đó \[1,45\] triệu đồng.
Lời giải
Hướng dẫn giải
Đáp án:
a) Sai.
b) Đúng.
c) Sai.
d) Đúng.
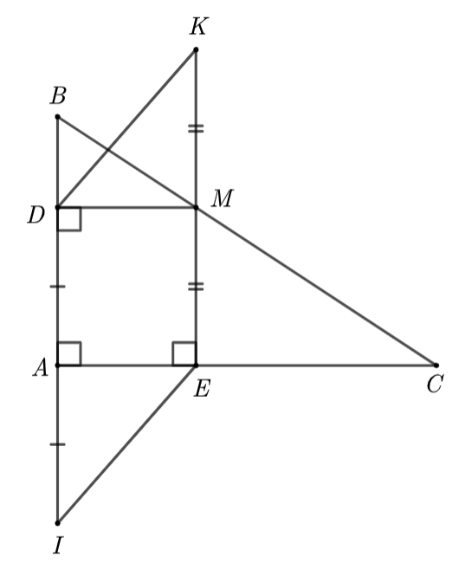
⦁ Khi lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
Suy ra \(AI = AD\,;\,\,MK = ME.\) Do đó ý a) là sai.
⦁ Xét tứ giác \(ADME\) có:
\(\widehat {DAE} = 90^\circ \) (vì \(\Delta ABC\) vuông tại \(A\))
\(\widehat {ADM} = 90^\circ \) \(\left( {MD \bot AB} \right)\)
\(\widehat {AEM} = 90^\circ \) \(\left( {ME \bot AC} \right)\)
Do đó tứ giác \(ADME\) là hình chữ nhật. Do đó ý b) đúng.
⦁ Vì \(AB \bot AC\) (vì \(\Delta ABC\) vuông tại \(A\)); \(MD \bot AB\) nên \(MD\,{\rm{//}}\,AC.\)
Tứ giác \(ADMC\) có \(MD\,{\rm{//}}\,AC\) nên \(ADMC\) là hình thang.
Hình thang \(ADMC\) có \(\widehat {CAD} = 90^\circ \) nên \(ADMC\) là hình thang vuông. Do đó ý c) sai.
⦁ Vì \(ADME\) là hình chữ nhật nên \(AD = ME\,;\,\,AD\,{\rm{//}}\,ME\) (tính chất hình chữ nhật).
Mà \(A\) là trung điểm của \(DI\); \(M\) là trung điểm của \(KE\) nên \[DI = KE;\,\,DI\,{\rm{//}}\,KE.\]
Suy ra \(DIEK\) là hình bình hành.
Do đó \(DK\,{\rm{//}}\,EI\). Do đó ý d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo