Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\) là một điểm bất kì trên cạnh huyền \(BC\). Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống \(AB\) và \(AC.\) Lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
a) \(IA = ID\,;\,\,KM = KE.\)
b) Tứ giác \(ADME\) là hình chữ nhật.
c) Tứ giác \(ADMC\) là hình thang cân.
d) \(DK\,{\rm{//}}\,EI\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án:
a) Sai.
b) Đúng.
c) Sai.
d) Đúng.
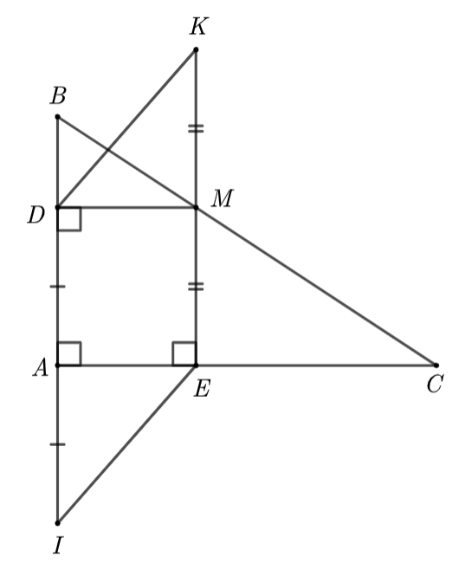
⦁ Khi lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
Suy ra \(AI = AD\,;\,\,MK = ME.\) Do đó ý a) là sai.
⦁ Xét tứ giác \(ADME\) có:
\(\widehat {DAE} = 90^\circ \) (vì \(\Delta ABC\) vuông tại \(A\))
\(\widehat {ADM} = 90^\circ \) \(\left( {MD \bot AB} \right)\)
\(\widehat {AEM} = 90^\circ \) \(\left( {ME \bot AC} \right)\)
Do đó tứ giác \(ADME\) là hình chữ nhật. Do đó ý b) đúng.
⦁ Vì \(AB \bot AC\) (vì \(\Delta ABC\) vuông tại \(A\)); \(MD \bot AB\) nên \(MD\,{\rm{//}}\,AC.\)
Tứ giác \(ADMC\) có \(MD\,{\rm{//}}\,AC\) nên \(ADMC\) là hình thang.
Hình thang \(ADMC\) có \(\widehat {CAD} = 90^\circ \) nên \(ADMC\) là hình thang vuông. Do đó ý c) sai.
⦁ Vì \(ADME\) là hình chữ nhật nên \(AD = ME\,;\,\,AD\,{\rm{//}}\,ME\) (tính chất hình chữ nhật).
Mà \(A\) là trung điểm của \(DI\); \(M\) là trung điểm của \(KE\) nên \[DI = KE;\,\,DI\,{\rm{//}}\,KE.\]
Suy ra \(DIEK\) là hình bình hành.
Do đó \(DK\,{\rm{//}}\,EI\). Do đó ý d) đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Một kho chứa có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 6 m và trung đoạn là \[3{\rm{ m}}.\] Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ p (ảnh 1)](https://video.vietjack.com/upload2/images/1752817036/1752817098-image6.png)
Lời giải
Hướng dẫn giải
Đáp số: \[{\bf{1}},{\bf{45}}\].
Nửa chu vi đáy của kho chứa là: \[\left( {6 \cdot \;4} \right):2 = 12\,\,\left( {\rm{m}} \right).\]
Diện tích xung quanh của kho chứa là: \[12 \cdot 3 = 36{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\]
Diện tích cần sơn phủ là: \[36 - 7 = 29{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right).\]
Số tiền cần trả để hoàn thành việc sơn phủ là:
\[29 \cdot 50{\rm{ }}000 = 1\,\,450\,\,000\] (đồng) \[ = 1,45\] (triệu đồng).
Vậy số tiền cần trả để hoàn thành việc sơn phủ đó \[1,45\] triệu đồng.
Lời giải
Hướng dẫn giải
Đáp số: \[ - {\bf{8}}\].
Ta có \[T = \left( {{x^2} - 6x + 12} \right)\left( {x - 6} \right) - {\left( {x - 4} \right)^3}\]
\[ = {x^3} - 6{x^2} + 12x - 6{x^2} + 36x - 72 - \left( {{x^3} - 12{x^2} + 48x - 64} \right)\]
\[ = {x^3} - 12{x^2} - 48x - 72 - {x^3} + 12{x^2} - 48x + 64\]
\( = \left( {{x^3} - {x^3}} \right) + \left( {12{x^2} - 12{x^2}} \right) + \left( {48x - 48x} \right) + \left( {64 - 72} \right)\)\( = - 8\).
Vậy \(T = - 8.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo