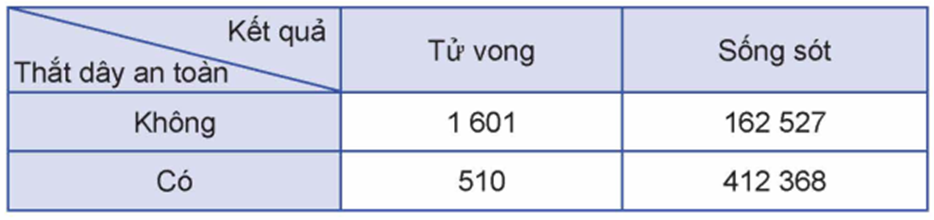
(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

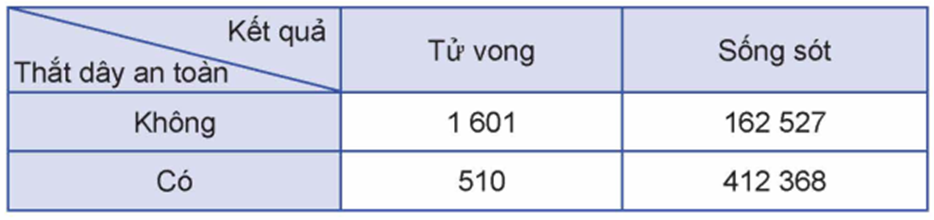
- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

                         

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

So sánh hai xác suất ở câu \(a\) và câu b rồi rút ra kết luận.

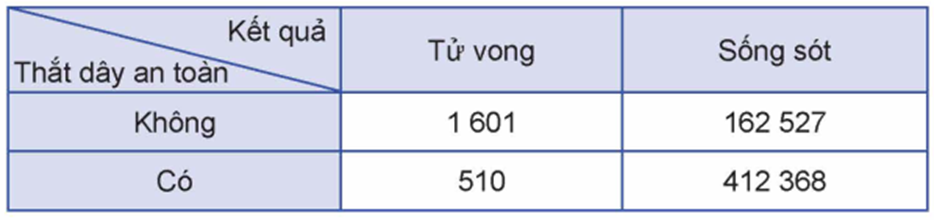
(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

Tính xác suất để người lái xe đó tử vong khi xảy ra tai nạn giao thông trong trường hợp không thắt dây an toàn.

(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

Tính xác suất để người lái xe đó tử vong khi xảy ra tai nạn giao thông trong trường hợp có thắt dây an toàn.

Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có \(56\% \) số học sinh thích kem, \(68\% \) số học sinh thích trà sữa, \(24\% \) số học sinh thích cả trà sửa và kem (Hình 6.2). Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa.

 

Một công ty vừa ra mắt sản phẩm \(X\) và tổ chức ngày trải nghiệm sản phẩm. Họ thống kê được trong 200 người đến tham quan ngày trải nghiệm có 60 người là nam giới và 140 người là nữ giới. Trong số những người được thống kê này, có 120 người mua sản phẩm X , gồm 40 khách hàng nam và 80 khách hàng nữ, còn lại là không mua sản phẩm X. Chọn ngẫu nhiên một người trong số 200 người được thống kê. Tính xác suất để người này mua sản phẩm \(X\), biết rằng người được chọn là nữ giới (làm tròn kết quả đến hàng phần trăm).

Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc \(X\) và thuốc \(Y\), người ta tiến hành thử nghiệm trên 4000 người bệnh tình nguyện. Kết quả được cho trong bảng thống kê \(2 \times 2\) sau:

Chọn ngẫu nhiên 1 người bệnh tham gia tình nguyện thử nghiệm thuốc.

Tính xác suất để người đó khỏi bệnh nếu biết người bệnh đó uống thuốc \(X\).

Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh \(X\) của hai loại thuốc M và N . Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân dùng thuốc \({\rm{M}},1600\) bệnh nhân còn lại dùng thuốc N . Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau: