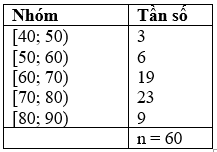
Cho bảng tần số ghép nhóm thống kê mức lương của một công ty ( đơn vị: triệu đồng)

a) Tính khoảng biến thiên của mẫu số liệu trên là:
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
Cho bảng tần số ghép nhóm thống kê mức lương của một công ty ( đơn vị: triệu đồng)

a) Tính khoảng biến thiên của mẫu số liệu trên là:
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
Quảng cáo
Trả lời:
a) Trong mẫu số liệu ghép nhóm ở bảng, ta có: đầu mút trái của nhóm 1 là \({{\rm{a}}_1} = 10\), đầu mút phải của nhóm 6 là \({{\rm{a}}_7} = 40\).
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
\({\rm{R}} = {{\rm{a}}_7} - {{\rm{a}}_1} = 40 - 10 = 30{\rm{ ((triệu đồng))}}{\rm{. }}\)
b) Từ Bảng trên ta có bảng sau:
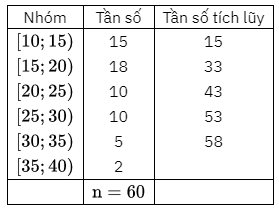
Số phần tử của mẫu là \({\rm{n}} = 60\).
Ta có: \(\frac{n}{4} = \frac{{60}}{4} = 15\). Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15 . Xét nhóm 1 là nhóm \([10;15)\) có \({\rm{s}} = 10;{\rm{h}} = 5;{{\rm{n}}_1} = 15\).
Áp dụng công thức, ta có tứ phân vị thứ nhất là: \({Q_1} = 10 + \frac{{15}}{{15}} \cdot 5 = 15\)(triệu đồng)
Ta có: \(\frac{{3n}}{4} = \frac{{3.60}}{4} = 45\) mà \(43 < 45 < 53\). Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lūy lớn hơn hoặc bẳng 45 . Xét nhóm 4 là nhóm \([25;30)\) có \(t = 25;1 = 5;{n_4} = 10\) và nhóm 3 là nhóm \([20;25)\) có cf \(3 = 43\).
Áp dụng công thức, ta có tứ phân vị thứ ba là: \({Q_3} = 25 + \left( {\frac{{45 - 43}}{{10}}} \right) \cdot 5 = 26{\rm{ }}\)(triệu đồng)
Vậy khoảng tứ phân vị của mẵu số liệu ghép nhóm đã cho là: \({\Delta _Q} = {Q_3} - {Q_1} = 26 - 15 = 11\)(triệu đồng)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
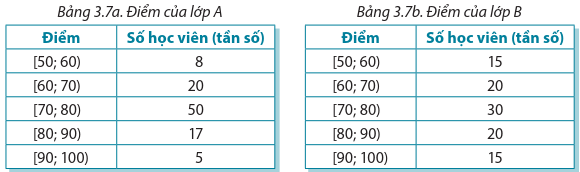
Khoảng biến thiên là: \({R_2} = 110 - 40 = 70\).
Cỡ mẫu là \(n = 20\).
Gọi \({x_1};{x_2}; \ldots ;{x_{20}}\) là số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 2022 và được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu là \(\frac{{{x_5} + {x_6}}}{2}\).
Mà \({x_5};{x_6}\) thuộc nhóm [50 ; 60) nên nhóm chứa tứ phân vị thứ nhất là [50 ; 60).
Ta có \({Q_1} = 50 + \frac{{\frac{{20}}{4} - 2}}{5} \cdot (60 - 50) = 56\).
Tứ phân vị thứ ba của mẫu số liệu là \(\frac{{{x_{15}} + {x_{16}}}}{2}\).
Mà \({x_{15}}\) : \({x_{16}}\) thuộc nhóm [70 ; 80) nên nhóm chứa tứ phân vị thứ ba là [70 ; 80).
Ta có \({Q_3} = 70 + \frac{{\frac{{20.3}}{4} - 14}}{5} \cdot (80 - 70) = 72\).
Do đó \({{\rm{D}}_{2{\rm{Q}}}} = 72 - 56 = 16\).
Giá trị chính xác là \({R_1}\) và \({{\rm{D}}_{1Q}}\); giá trị xấp xỉ là \({R_2}\) và \({{\rm{D}}_{2Q}}\).
Lời giải
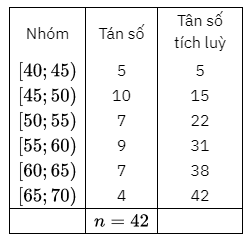
Cỡ mẫu là \(n = 42\).
Ta có: \(\frac{n}{4} = \frac{{42}}{4} = 10,5\) mà \(5 < 10,5 < 15\). Suy ra nhóm 2 là nhóm đẩu tiên có tẩn số tích lũy lớn hơn hoặc bằng 10,5 .
Tứ phân vị thứ nhất: \({Q_1} = 45 + \left( {\frac{{10,5 - 5}}{{10}}} \right) \cdot 5 = 47,75(\;{\rm{cm}}).\)
Tứ phân vị thứ ba là: \({Q_3} = 60 + \left( {\frac{{31,5 - 31}}{7}} \right).5 \approx 60,4(\;{\rm{cm}}).\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là: \({\Delta _Q} = {Q_3} - {Q_1} \approx 60,4 - 47,75 = 12,65(\;{\rm{cm}}).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.