Câu hỏi:
13/07/2024 17,270Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân.
Quảng cáo
Trả lời:
Giải bởi Vietjack
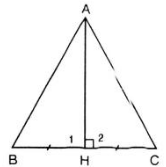
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
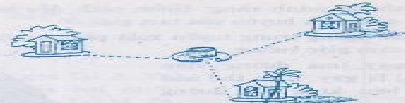
Gọi vị trí ba ngôi nhà lần lượt là A, B, C, vị trí giếng cần đào là O.
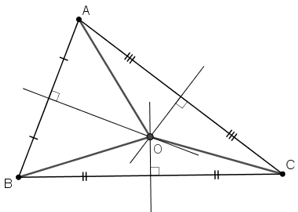
Vì điểm O cách đều ba điểm A, B, C nên O là giao của ba đường trung trực của AB, BC, CA (hay O là tâm đường tròn ngoại tiếp tam giác ABC).
Tuy nhiên để xác định O ta chỉ cần xác định hai trong ba đường trung trực rồi cho chúng cắt nhau vì ba đường trung trực đều đồng quy tại một điểm.
Lời giải
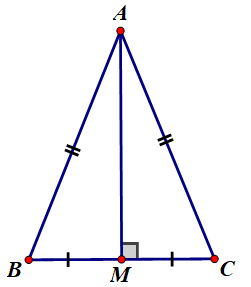
- Giả thiết : ΔABC cân tại A
AM là đường trung trực ứng với cạnh BC
- Kết luận : AM là trung tuyến ứng với cạnh BC
Nhắn tin Zalo
Dương Bùi
Nếu là trường hợp đặc biệt thì cạnh huyền của tam giác là AB Và AC mà
Dương Bùi
Trường hợp sai nốt có 3 trường hợp thường của tam giác và 2 trường hợp đặc biệt của tam giác thôi
Xem tất cả 1 phản hồi
Huu Luan Nguyen
có 4 trường hợp đặc biệt lận
Dương Bùi
Sai rồi cần 3 điều kiện để CM 2 tam giác bằng nhau
Xem tất cả 1 phản hồi
Anh Pham
bài nào vậy