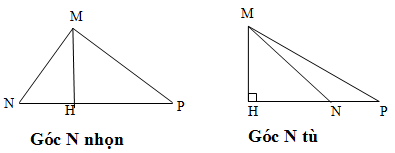
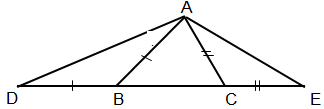
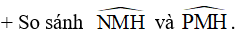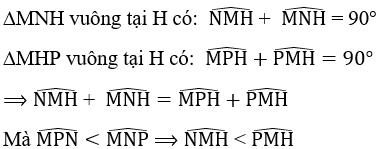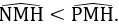Gọi MH là đường cao của tam giác MNP. Chứng minh rằng:
Nếu MN<MP thì HN<HP và
(yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).
Quảng cáo
Trả lời:
Giải bởi Vietjack
+ So sánh NH và PH
MH là đường cao của ΔMNP ⇒ H là hình chiếu của M trên đường thẳng NP.
⇒ NH là hình chiếu của đường xiên NM trên đường thẳng NP
PH là hình chiếu của đường xiên MP trên đường thẳng NP.
Mà NM < PM ⇒ NH < PH (đường xiên nào lớn hơn thì hình chiếu lớn hơn).
• TH1: Xét ΔMNP có góc N nhọn
⇒ góc P nhọn (vì MN < MP nên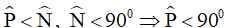 
).
⇒ H nằm giữa N và P.
• TH2: Xét ΔMNP có góc N tù
suy ra H nằm ngoài cạnh NP.
(vì giả sử H nằm giữa N và P thì ΔMNH có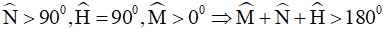 
).
Lại có HN < HP nên N nằm giữa H và P
⇒ Tia MN ở giữa hai tia MH và MP ⇒ 
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
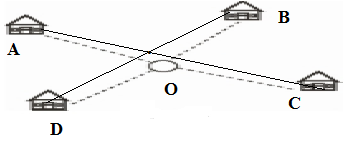
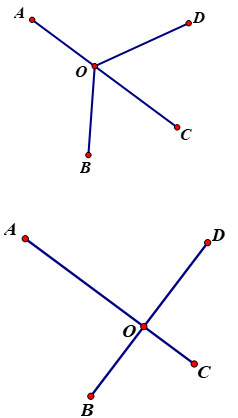
Gọi O là địa điểm đặt nhà máy (O tùy ý)
A, B, C, D lần lượt là bốn điểm dân cư (A,B, C, D cố định).
Ta luôn có:
OA + OC ≥ AC
OB + OD ≥ BD
⇒ OA + OB + OC + OD ≥ AC + BD (AC + BD là hằng số)
Vậy để OA + OB + OC + OD nhỏ nhất thì OA + OC = AC và OB + OD = BD.
OA + OC = AC khi O thuộc đoạn AC.
OB + OD = BD khi O thuộc đoạn BD.
Vậy OA + OB + OC + OD nhỏ nhất khi O là giao điểm của hai đoạn AC và BD.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập