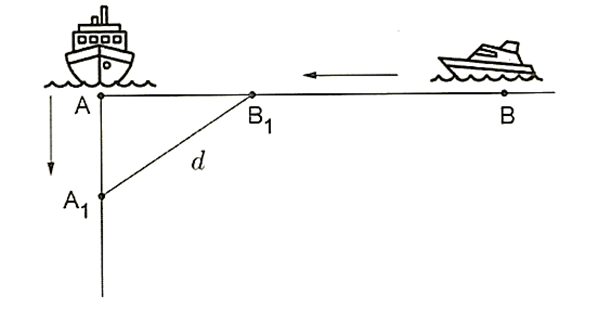
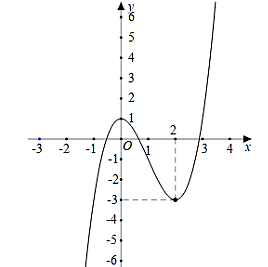Hai con tàu \(A\) và \(B\) đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu \(A\) chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu \(B\) chạy về vị trí hiện tại của tàu \(A\) với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?
Hai con tàu \(A\) và \(B\) đang ở cùng một vĩ tuyến và cách nhau 6 hải lí. Cả hai tàu đồng thời cùng khởi hành. Tàu \(A\) chạy về hướng Nam với vận tốc 5 hải lí/ giờ, còn tàu \(B\) chạy về vị trí hiện tại của tàu \(A\) với vận tốc 7 hải lí/ giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là bé nhất (làm tròn kết quả đến hàng phần trăm)?

Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 12 có đáp án !!
Quảng cáo
Trả lời:
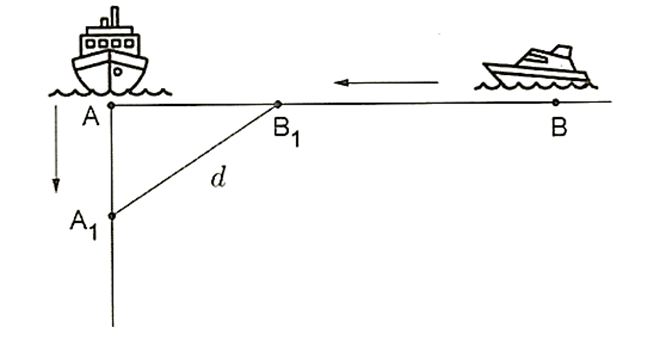
Giả sử ban đầu tàu \(A\) ở vị trí \(A\) và tàu \(B\) ở vị trí \(B\). Sau khoảng thời gian \(t\):
Tàu \(A\) di chuyển được quãng đường \(5t\) về phía Nam đến vị trí \({A_1}\).
Tàu \(B\) di chuyển được quãng đường \(7t\) đến vị trí \({B_1}\).
Khoảng cách từ vị trí \({B_1}\) đến vị trí \[A\] là \(6 - 7t\).
Áp dụng định lý Pytago ta có: \(d = {A_1}{B_1} = f\left( t \right) = \sqrt {{{\left( {6 - 7t} \right)}^2} + {{\left( {5t} \right)}^2}} = \sqrt {74{t^2} - 84t + 36} \).
Để khoảng cách giữa hai tàu nhỏ nhất, thì hàm số \(g\left( t \right) = 74{t^2} - 84t + 36\) đạt giá trị nhỏ nhất.
Hàm số \(g\left( t \right)\) đạt giá trị nhỏ nhất tại \(t = \frac{{ - \left( { - 84} \right)}}{{2.74}} = \frac{{21}}{{37}}\), vậy thời điểm khoảng cách giữa hai tàu bé nhất là khi \(t = \frac{{21}}{{37}} \approx 0,57\)(giờ).
Đáp án: \(0,57\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
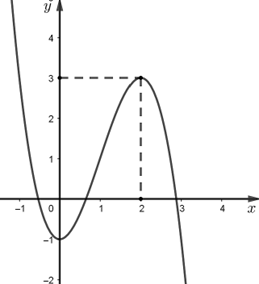
a) Đúng. Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu của hàm số \(f\left( x \right)\) bằng \( - 1\).
b) Đúng. Ta có: \({\log _3}\left( {f\left( x \right) + 6} \right) = 2 \Leftrightarrow f\left( x \right) + 6 = 9 \Leftrightarrow f\left( x \right) = 3\) \(\left( * \right)\)
Số nghiệm của phương trình \(\left( * \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với đường thẳng \(y = 3\). Dựa vào đồ thị ta thấy phương trình \(\left( * \right)\) có 2 nghiệm.
c) Sai. Dựa vào đồ thị ta thấy hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1;2} \right)\) và nghịch biến trên khoảng \(\left( {2;3} \right)\).
d) Đúng. Ta có \(f'\left( x \right) = 3a{x^2} + 2bx + c\).
Theo giả thiết ta có: \(\left\{ \begin{array}{l}f'\left( 0 \right) = 0\\f'\left( 2 \right) = 0\\f\left( 0 \right) = - 1\\f\left( 2 \right) = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\12a + 4b + c = 0\\d = - 1\\8a + 4b + 2c + d = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 3\\c = 0\\d = - 1\end{array} \right.\).
Tổng \(2025a + b + c + d = - 2025 + 3 + 0 - 1 = - 2023\).
Lời giải
Do \(I\) là trọng tâm tam giác \(GBC\) nên ta có: \(\overrightarrow {SI} = \frac{1}{3}\left( {\overrightarrow {SG} + \overrightarrow {SB} + \overrightarrow {SC} } \right)\,\,\,\,\,\,\,\left( 1 \right)\).
Do \(G\) là trọng tâm tam giác \(ABC\) nên ta có: \(\overrightarrow {SG} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right)\,\,\,\,\,\left( 2 \right)\).
Thay \(\left( 2 \right)\) vào \(\left( 1 \right)\) ta có: \(\overrightarrow {SI} = \frac{1}{3}\left( {\frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) + \overrightarrow {SB} + \overrightarrow {SC} } \right) = \frac{1}{9}\overrightarrow {SA} + \frac{4}{9}\overrightarrow {SB} + \frac{4}{9}\overrightarrow {SC} \).
Vậy \(\left\{ \begin{array}{l}x = \frac{1}{9}\\y = \frac{4}{9}\\z = \frac{4}{9}\end{array} \right. \Rightarrow 9\left( {x - y + z} \right) = 1\).
Đáp án: 1.
Câu 3
A. \( - 3\).
B. \(2\).
C. \(1\).
D. \(0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[y = 1 - 2x\].
B. \[y = 2x\].
C. \[y = 2x - 1\].
D. \[y = - 2x\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
B. \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
C. \(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
D. \(\overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {SD} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.