PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Trong hộp có 15 viên bi trắng, 5 viên bi đen có kích thước và khối lượng như nhau. Xét phép thử lấy ngẫu nhiên từ trong hộp 3 viên bi.
a) Số phần tử của không gian mẫu là \[n\left( \Omega \right) = 1140\].
b) Xác suất để chọn được 3 viên bi cùng màu là \(\frac{{35}}{{76}}\).
c) Xác suất để trong 3 viên bi được chọn có đúng 2 viên bi trắng là \(\frac{7}{{76}}\).
d) Xác suất để để trong 3 viên bi được chọn có ít nhất một viên bi đen là \(\frac{{137}}{{228}}\).
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 11 có đáp án !!
Quảng cáo
Trả lời:
a) Đúng. Ta có \[n\left( \Omega \right) = C_{20}^3 = 1140\].
b) Sai. Gọi biến cố A: “Chọn được 3 viên bi cùng màu”.
Có \[n\left( A \right) = C_{15}^3 + C_5^3 = 465 \Rightarrow P\left( A \right) = \frac{{465}}{{1140}} = \frac{{31}}{{76}}\].
c) Sai. Gọi biến cố B: “Chọn có đúng 2 viên bi trắng”.
Có \[n\left( B \right) = C_{15}^2C_5^1 = 525 \Rightarrow P\left( B \right) = \frac{{525}}{{1140}} = \frac{{35}}{{76}}\].
d) Đúng. Gọi biến cố C: “Chọn có ít nhất một viên bi đen”.
Có \[n\left( C \right) = C_{20}^3 - C_{15}^3 = 685 \Rightarrow P\left( C \right) = \frac{{685}}{{1140}} = \frac{{137}}{{228}}\].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
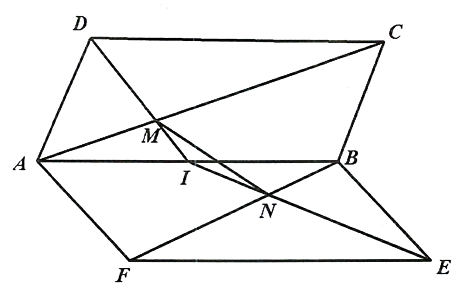
Ta có \(MN\,{\rm{//}}\,DE\) nên bốn điểm \(M,N,D,E\) đồng phẳng.
Trong mặt phẳng \(\left( {MNED} \right)\), gọi \(I = DM \cap NE \Rightarrow I \in AB,AB = \left( {ABCD} \right) \cap \left( {ABEF} \right)\).
Khi đó: \(\frac{{IM}}{{DM}} = \frac{{IN}}{{NE}}\).
Theo giả thiết, ta có: \(\frac{{AM}}{{AC}} = k\,\,(1) \Rightarrow \frac{{AC - MC}}{{AC}} = k \Rightarrow 1 - \frac{{MC}}{{AC}} = k \Rightarrow \frac{{MC}}{{AC}} = 1 - k\,\,(2).\)
Từ (1) và (2) suy ra \(\frac{{AM}}{{MC}} = \frac{k}{{1 - k}}\); tương tự ta chứng minh được \(\frac{{BN}}{{FN}} = \frac{k}{{1 - k}}\).
Vì \(AB\,{\rm{//}}\,CD\) nên \(\frac{{IM}}{{DM}} = \frac{{IA}}{{DC}} = \frac{{AM}}{{MC}} = \frac{k}{{1 - k}}\);
Vì \(AB\,{\rm{//}}\,EF\) nên \(\frac{{IN}}{{NE}} = \frac{{BI}}{{EF}} = \frac{{BN}}{{NF}} = \frac{k}{{1 - k}}\).
Mặt khác \(\frac{{AI}}{{DC}} + \frac{{BI}}{{EF}} = \frac{{AI}}{{FE}} + \frac{{BI}}{{EF}} = 1 \Rightarrow 2 \cdot \frac{k}{{1 - k}} = 1\)\( \Rightarrow 2k = 1 - k \Rightarrow k = \frac{1}{3}{\rm{. }}\)
Vậy với \(k = \frac{1}{3}\) thì \(MN\,{\rm{//}}\,DE\).
Lời giải
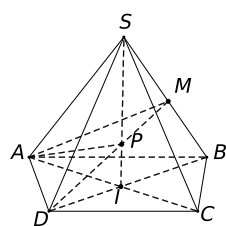
Ta có \(P = MD \cap SI\). Khi đó, \(\left\{ \begin{array}{l}P \in MD,MD \subset \left( {ADM} \right)\\P \in SI,SI \subset \left( {SAC} \right)\end{array} \right. \Rightarrow P \in \left( {ADM} \right) \cap \left( {SAC} \right).\)
Ngoài ra \(A \in \left( {ADM} \right) \cap \left( {SAC} \right)\), do đó \(\left( {ADM} \right) \cap \left( {SAC} \right) = AP.\)Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.