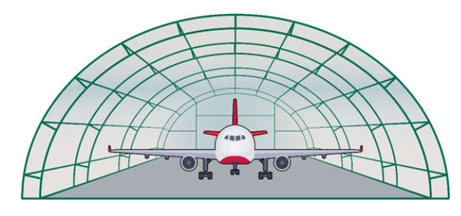
Nhà vòm chứa máy bay có mặt cắt đứng là một nửa hình elip cao 10 m và rộng 24 m. Tính khoảng cách theo phương thẳng đứng từ một điểm trên sàn nhà cách chân tường 4 m lên đến mái vòm.
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn hệ tọa độ như hình vẽ.
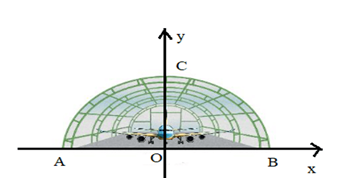
Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\).
Chiều cao vòm là \(10\,{\rm{m}}\) nên \(OC = b = 10\), chiều rộng của vòm là \(24\,{\rm{m}}\)nên \(AB = 2a = 24 \Rightarrow a = 12\).
Khi đó phương trình elip là: \(\frac{{{x^2}}}{{144}} + \frac{{{y^2}}}{{100}} = 1\).
Gọi D là điểm thuộc elip có hình chiếu trên sàn là điểm H cách chân tường 4 m.
Điểm H cách chân tường 4 m tương ứng cách tâm O là 8 m (vì từ tâm O đến tường là 12 m) \( \Rightarrow D\left( {8;{y_D}} \right)\). Thay tọa độ của D vào phương trình elip ta được: \(\frac{{{8^2}}}{{144}} + \frac{{{y_D}^2}}{{100}} = 1\)\( \Rightarrow {y_D} = \frac{{10\sqrt 5 }}{3}\).
Vậy khoảng cách theo phương thẳng đứng từ một điểm trên sàn nhà cách chân tường 4 m lên đến mái vòm là \(\frac{{10\sqrt 5 }}{3}\) m.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
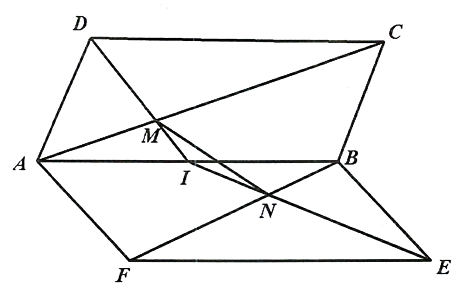
Ta có \(MN\,{\rm{//}}\,DE\) nên bốn điểm \(M,N,D,E\) đồng phẳng.
Trong mặt phẳng \(\left( {MNED} \right)\), gọi \(I = DM \cap NE \Rightarrow I \in AB,AB = \left( {ABCD} \right) \cap \left( {ABEF} \right)\).
Khi đó: \(\frac{{IM}}{{DM}} = \frac{{IN}}{{NE}}\).
Theo giả thiết, ta có: \(\frac{{AM}}{{AC}} = k\,\,(1) \Rightarrow \frac{{AC - MC}}{{AC}} = k \Rightarrow 1 - \frac{{MC}}{{AC}} = k \Rightarrow \frac{{MC}}{{AC}} = 1 - k\,\,(2).\)
Từ (1) và (2) suy ra \(\frac{{AM}}{{MC}} = \frac{k}{{1 - k}}\); tương tự ta chứng minh được \(\frac{{BN}}{{FN}} = \frac{k}{{1 - k}}\).
Vì \(AB\,{\rm{//}}\,CD\) nên \(\frac{{IM}}{{DM}} = \frac{{IA}}{{DC}} = \frac{{AM}}{{MC}} = \frac{k}{{1 - k}}\);
Vì \(AB\,{\rm{//}}\,EF\) nên \(\frac{{IN}}{{NE}} = \frac{{BI}}{{EF}} = \frac{{BN}}{{NF}} = \frac{k}{{1 - k}}\).
Mặt khác \(\frac{{AI}}{{DC}} + \frac{{BI}}{{EF}} = \frac{{AI}}{{FE}} + \frac{{BI}}{{EF}} = 1 \Rightarrow 2 \cdot \frac{k}{{1 - k}} = 1\)\( \Rightarrow 2k = 1 - k \Rightarrow k = \frac{1}{3}{\rm{. }}\)
Vậy với \(k = \frac{1}{3}\) thì \(MN\,{\rm{//}}\,DE\).
Lời giải
Ta có \(P = MD \cap SI\). Khi đó, \(\left\{ \begin{array}{l}P \in MD,MD \subset \left( {ADM} \right)\\P \in SI,SI \subset \left( {SAC} \right)\end{array} \right. \Rightarrow P \in \left( {ADM} \right) \cap \left( {SAC} \right).\)
Ngoài ra \(A \in \left( {ADM} \right) \cap \left( {SAC} \right)\), do đó \(\left( {ADM} \right) \cap \left( {SAC} \right) = AP.\)Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo