Một bình thuỷ tinh chứa không khí được đậy kín bằng một nút có khối lượng m. Tiết diện của miệng bình là \(S = 1,5{\rm{\;c}}{{\rm{m}}^2}\). Khi ở nhiệt độ phòng \(\left( {{{27}^ \circ }{\rm{C}}} \right)\) người ta xác định được áp suất của khối khí trong bình bằng với áp suất khí quyển và bằng 1 atm. Đun nóng bình tới nhiệt độ \({87^ \circ }{\rm{C}}\) thì người ta thấy nút bị đẩy lên. Tính khối lượng m của nút, cho gia tốc trọng trường \(g = 10{\rm{\;m/}}{{\rm{s}}^2}\).

Quảng cáo
Trả lời:
Phương pháp:
- Áp dụng công thức trong quá trình đẳng tích: \(\frac{P}{T} = \) const.
- Áp suất của khí ở trạng thái 2: \(p = {p_0} + \frac{{mg}}{S}\).
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1} = 101325\left( {Pa} \right)}\\{{T_1} = 27 + 273 = 300\left( K \right)}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = {p_0} + \frac{{mg}}{S} = 101325 + \frac{{m.10}}{{{{1,5.10}^{ - 4}}}}}\\{{T_2} = 87 + 273 = 3609K}\end{array}} \right.\)
Vì thể tích không đổi nên \(\frac{p}{T} = \)const
\( \Rightarrow \frac{{101325}}{{300}} = \frac{{101325 + \frac{{m.10}}{{{{1,5.10}^{ - 4}}}}}}{{360}}\)
\( \Rightarrow m \approx 0,304\left( {{\rm{kg}}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
- Áp dụng nguyên lý bình thông nhau, áp suất tại các điểm khác nhau của cùng một chất lỏng nằm trên cùng một mặt phẳng nằm ngang bằng nhau.
- Áp dụng định luật Boyle: \(pV = \) const.
Cách giải:
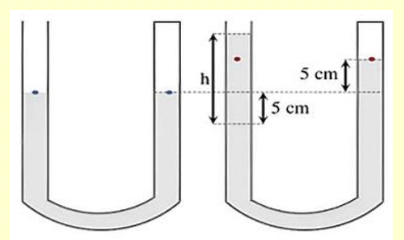
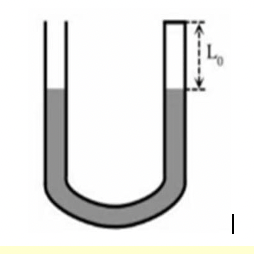
Áp suất tại hai điểm màu đỏ bằng nhau và đều bằng áp suất khí quyển p0.
Thủy ngân bên nhánh phải dâng lên \(30 - 25 = 5\left( {{\rm{cm}}} \right)\)
Theo nguyên lý bình thông nhau, áp suất tại hai điểm màu đỏ bằng nhau: \( \Rightarrow p = {p_0} + h - 10\)
Trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{p_1} = {p_0} = 75{\rm{cmHg}}}\\{{V_1} = S.{L_0} = S.30}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = {p_0} + h - 10 = 75 + h - 10 = 65 + h\left( {cmHg} \right)}\\{{V_2} = S.L = S.25}\end{array}} \right.\)
Vì nhiệt độ không đổi nên áp dụng định luật Boyle:
\({p_1}{V_1} = {p_2}{V_2} \Rightarrow 75.30 = \left( {65 + h} \right).25 \Rightarrow h = 25\left( {{\rm{cm}}} \right)\)
Lời giải
Lý thuyết về các cách làm thay đổi nội năng và nội năng.
Cách giải:
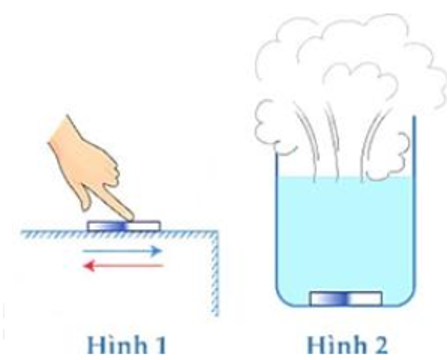
a) Hình 1 thể hiện quá trình thực hiện công.
\( \to \)a sai.
b) Hình b thể hiện quá trình truyền nhiệt.
\( \to \) b sai.
c) Trong quá trình thực hiện công, có sự chuyển hóa từ một dạng năng lượng khác sang nội năng.
Ví dụ: Hình 1: Cơ năng sang nội năng.
\( \to \) c đúng.
d) Trong quá trình truyền nhiệt, không có sự chuyển hóa các dạng năng lượng khác sang nội năng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
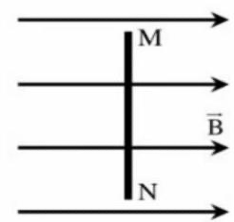
A. chiều từ M đến N và cường độ \(7,5{\rm{\;A}}\)
B. chiều từ N đến M và cường độ \(7,5{\rm{\;A}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Các chất không thể chuyển từ thể này sang thể khác.
B. Các chất có thể chuyển từ thể này sang thể khác.
C. Các chất chỉ có thể chuyển từ thể rắn sang thể lỏng mà không thể chuyển sang thể khí hay ngược lại.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.