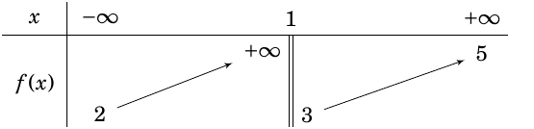
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 1}}{{2x - 1}}\), gọi \(I\) là giao điểm của đường tiện cận đứng và đường tiệm   cận xiên của đồ thị hàm số \(y = f\left( x \right)\), tổng hoành độ và tung độ của điểm \(I\) bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?

Gọi chiều rộng của đáy bể bơi là \(x,\,x > 0.\) Suy ra, chiều dài của đáy bể bơi là \(3x.\)

\(h\) là chiều cao của bể bơi \(\left( {h > 0} \right).\)

Theo giả thiết: \(V = 150 \Leftrightarrow h \cdot 3{x^2} = 150 \Leftrightarrow h = \frac{{150}}{{3{x^2}}} = \frac{{50}}{{{x^2}}}.\)

Diện tích các mặt bên và mặt đáy bể bơi là: \(S = 2hx + 6hx + 3{x^2} = 8hx + 3{x^2} = \frac{{400}}{x} + 3{x^2}\).

Ta có: \(S' = - \frac{{400}}{{{x^2}}} + 6x = \frac{{6{x^3} - 400}}{{{x^2}}}\); \(S' = 0 \Leftrightarrow x = \sqrt[3]{{\frac{{400}}{6}}} \approx 4,05\).

Lập BBT suy ra S đạt GTNN khi \(x = 4,05{\rm{ m}}{\rm{.}}\)

Vậy chiều rộng của đáy bể bơi là \(x = 4,05{\rm{ m}}\) để khi thi công tiết kiệm nguyên vật liệu nhất.

Đáp án: 4,05.

Gọi \({A_1},\,{B_1},\,{C_1}\) lần lượt là các điểm sao cho \(\overrightarrow {O{A_1}} = \overrightarrow {{F_1}} ,\,\,\overrightarrow {O{B_1}} = \overrightarrow {{F_2}} ,\,\overrightarrow {O{C_1}} = \overrightarrow {{F_3}} \). Lấy các điểm \({D_1},{A'_1},\,{B'_1},\,{D'_1}\) sao cho \(O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}{B'_1}\) là hình hộp như hình dưới đây.

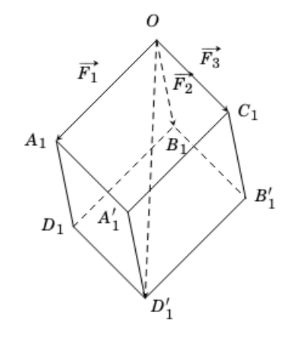
Theo quy tắc hình hộp, ta có: \(\overrightarrow {O{A_1}} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} = \overrightarrow {O{{D'}_1}} \).

Mặt khác, do các lực căng \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) đôi một vuông góc và \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 15\) (N) nên hình hộp \(O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}{B'_1}\) có ba cạnh \(O{A_1},\,O{B_1},\,O{C_1}\) đôi một vuông góc và bằng nhau.

Do đó, hình hộp \(O{A_1}{D_1}{B_1}.{C_1}{A'_1}{D'_1}{B'_1}\) là hình lập phương có độ dài cạnh bằng 15.

Suy ra độ dài đường chéo của hình lập phương đó bằng \(15\sqrt 3 \).

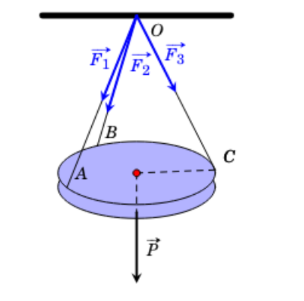
Do chiếc đèn ở vị trí cân bằng nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \), ở đó \(\overrightarrow P \) là trọng lực tác dụng lên chiếc đèn.

Vậy trọng lượng của chiếc đèn là \(\left| {\overrightarrow P } \right| = \left| {\overrightarrow {O{{D'}_1}} } \right| = 15\sqrt 3 \) (N).