C. TRẢ LỜI NGẮN
Một chuyển động xác định bởi phương trình \(S\left( t \right) = \frac{1}{3}{t^3} - 3{t^2} + 5t + 2\) với \[t \ge 0\], trong đó \[t\] tính bằng giây và \[s\]tính bằng mét. Biết bắt đầu từ giây thứ \({t_0}\) thì vận tốc của vật bắt đầu tăng. Tính \({t_0}.\)
Một chuyển động xác định bởi phương trình \(S\left( t \right) = \frac{1}{3}{t^3} - 3{t^2} + 5t + 2\) với \[t \ge 0\], trong đó \[t\] tính bằng giây và \[s\]tính bằng mét. Biết bắt đầu từ giây thứ \({t_0}\) thì vận tốc của vật bắt đầu tăng. Tính \({t_0}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vận tốc của chuyển động tại thời điểm \[t\] bằng đạo hàm cấp một của phương trình chuyển động tại thời điểm \[t\], ta có \(v\left( t \right) = S'\left( t \right) = {t^2} - 6t + 5\).
Xét hàm \(v\left( t \right) = {t^2} - 6t + 5\) với \[t \ge 0\]. Ta có \(v'\left( t \right) = 2t - 6;\) \(v'\left( t \right) = 0 \Leftrightarrow t = 3\).
Bảng biến thiên:
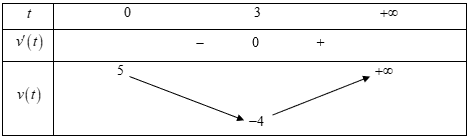
Từ bảng biến thiên, bắt đầu từ giây thứ \({t_0} = 3\) thì vận tốc của vật bắt đầu tăng.
Đáp án: 3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
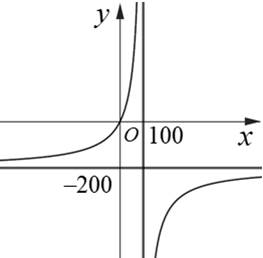
Ta có \(C\left( x \right) = \frac{{ax + b}}{{ - x + d}} \cdot \) Từ đồ thị suy ra \(b = 0\,;d = 100\,;\,a = 200 \Rightarrow C\left( x \right) = \frac{{200x}}{{100 - x}} \cdot \)
Chi phí chênh lệch là \(\Delta C = \left| {C\left( {99} \right) - C\left( {90} \right)} \right| = \left| {\frac{{200 \cdot 99}}{{100 - 99}} - \frac{{200 \cdot 90}}{{100 - 90}}} \right| = 18\,000\) (triệu đồng) \( = 18\) (tỉ đồng).
Đáp án: 18.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \[M\left( {{x_0};{y_0}} \right) \in \left( C \right) \Rightarrow M\left( {{x_0};\frac{{x_0^2 + 4{x_0} + 5}}{{{x_0} + 2}}} \right)\].
Gọi \[\left( d \right)\] là khoảng cách từ \[M\] đến đường thẳng \[3x + y + 6 = 0\].
Ta có \[d = \frac{1}{{\sqrt {10} }}\left| {\frac{{4x_0^2 + 16{x_0} + 17}}{{{x_0} + 2}}} \right| = \frac{1}{{\sqrt {10} }}\left| {4\left( {{x_0} + 2} \right) + \frac{1}{{{x_0} + 2}}} \right| \ge \frac{4}{{\sqrt {10} }}\].
Đẳng thức xảy ra \[ \Leftrightarrow 4\left| {{x_0} + 2} \right| = \frac{1}{{\left| {{x_0} + 2} \right|}} \Leftrightarrow \left[ \begin{array}{l}{x_0} = \frac{{ - 3}}{2} \Rightarrow {y_0} = \frac{5}{2}\\{x_0} = \frac{{ - 5}}{2} \Rightarrow {y_0} = - \frac{5}{2}\end{array} \right.\].
Vậy có hai điểm thoả yêu cầu bài toán là \[{M_1}\left( {\frac{{ - 3}}{2};\frac{5}{2}} \right)\] và \[{M_2}\left( {\frac{{ - 5}}{2};\frac{{ - 5}}{2}} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
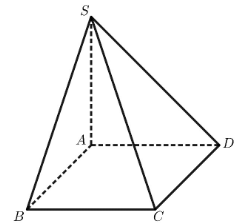
A. \(\overrightarrow {SA} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\left( { - 2\,; - 3} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập