Để đảm bảo an toàn trong quá trình sử dụng, nồi áp suất có van an toàn, cấu tạo gồm một lỗ tròn có diện tích \(1{\rm{\;c}}{{\rm{m}}^2}\) luôn được áp chặt bởi một lò xo có độ cứng \({10^3}{\rm{\;N/m}}\) và luôn bị nén 1 cm. Ban đầu khí trong nồi áp suất khí quyển là \({10^5}{\rm{\;N/}}{{\rm{m}}^2}\) và nhiệt độ \({20^ \circ }{\rm{C}}\). Xem như khí không thoát ra ngoài ở các vị trí khác. Van an toàn bắt đầu mở ra khi khí trong nồi có nhiệt độ nhỏ nhất là bao nhiêu\({\;^ \circ }{\rm{C}}\) (làm tròn kết quả đến chữ số hàng đơn vị)?

Để đảm bảo an toàn trong quá trình sử dụng, nồi áp suất có van an toàn, cấu tạo gồm một lỗ tròn có diện tích \(1{\rm{\;c}}{{\rm{m}}^2}\) luôn được áp chặt bởi một lò xo có độ cứng \({10^3}{\rm{\;N/m}}\) và luôn bị nén 1 cm. Ban đầu khí trong nồi áp suất khí quyển là \({10^5}{\rm{\;N/}}{{\rm{m}}^2}\) và nhiệt độ \({20^ \circ }{\rm{C}}\). Xem như khí không thoát ra ngoài ở các vị trí khác. Van an toàn bắt đầu mở ra khi khí trong nồi có nhiệt độ nhỏ nhất là bao nhiêu\({\;^ \circ }{\rm{C}}\) (làm tròn kết quả đến chữ số hàng đơn vị)?

Quảng cáo
Trả lời:
Phương pháp:
Sử dụng công thức tính áp suất: \(p = \frac{F}{S}\)
Vận dụng công thức tính lực đàn hồi: \(F = k{\rm{\Delta }}l\)
Quá trình trên là quá trình đẳng tích nên áp dụng biểu thức tương ứng: \(\frac{{{p_2}}}{{{T_2}}} = \frac{{{p_1}}}{{{T_1}}}\)
Cách giải:
Áp suất do lực đàn hồi của lò xo tác dụng lên van là:
\({p_v} = \frac{F}{S} = \frac{{k\left| x \right|}}{S} = \frac{{1000.0,01}}{{{{1.10}^{ - 4}}}} = 10000\left( {{\rm{N}}/{{\rm{m}}^2}} \right)\)
Áp suất mới cần để van mở ra khi đun nóng:
\({p_2} = {p_0} + {p_v} = 10000 + 10000 = 20000\left( {{\rm{N}}/{{\rm{m}}^2}} \right)\)
Quá trình trên thể tích không đổi nên ta có:
\(\frac{{{p_2}}}{{{T_2}}} = \frac{{{p_1}}}{{{T_1}}} \Rightarrow \frac{{20000}}{{{T_2}}} = \frac{{10000}}{{20 + 273}}\)
\( \Rightarrow {T_2} = \frac{{20000}}{{10000}}.\left( {20 + 273} \right) = 586{\rm{\;K}}\)
\( \Rightarrow {t_2} = 586 - 273 = {313^ \circ }{\rm{C}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. tăng đồng thời áp suất khí tăng.
B. giảm đồng thời áp suất khí giảm.
Lời giải
Phương pháp:
Áp dụng định luật Boyle
Cách giải:
Theo định luật Boyle ta có: \({\rm{pV}} = \) hằng số
Ban đầu, pittong sát đầu trên của xilanh (thể tích của khí nhỏ)
Sau đó kéo pittong thì thể tích khí ở bên trong xilanh tăng lên
Suy ra: V tăng thì p giảm
Suy ra: Thể tích khí trong xilanh tăng đồng thời áp suất khí giảm.
Câu 2
Lời giải
Phương pháp:
Vận dụng kiến thức về thang đo:
+ Tạo phương trình tương ứng giữa hai thang đo nhiệt độ X và Y, dựa trên mối quan hệ tuyến tính giữa các thang đo.
+ Công thức tổng quát cho sự chuyển đổi giữa hai thang đo
Cách giải:
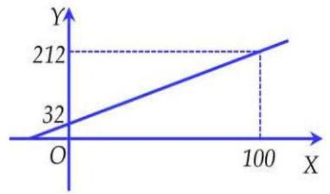
Ta có: \({T_Y} = a{T_X} + b\)
- Khi \({T_X} = 100X;{T_Y} = a.100 + b = 212Y\)
- Khi \({T_X} = 0X;{T_Y} = a.0 + b = 32Y\)
Giải hệ phương trình tìm được: \({\rm{a}} = 1,8;{\rm{b}} = 32\)
Thay các cặp giá trị đề bài đã cho vào biểu thức trên, ta xác định được: \({T_Y} = 1,8{T_X} + 32\)
Thay \({T_X} = 20X\) vào biểu thức vừa xác định, ta tính được: \({T_Y} = 68Y\)
Câu 3
A. b, d, e, c, a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Nhôm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.