Một khinh khí cầu có tổng khối lượng (gồm khoang và hành khách) là 450 kg. Phần khí cầu chứa \({3,00.10^3}{\rm{\;}}{{\rm{m}}^3}\) không khí. Biết khí quyển bên ngoài có nhiệt độ là \({25^ \circ }{\rm{C}}\) và áp suất là \({1,03.10^5}{\rm{\;Pa}}\), gia tốc trọng trường là \(g = 9,8{\rm{\;m/}}{{\rm{s}}^2}\).

     a) Lực tối thiểu để nâng khoang lên khỏi mặt đất là 4410 N.

     b) Khinh khí cầu bay lên được là do khối lượng riêng của khí trong khí cầu nhỏ hơn của khí quyển.

     c) Coi không khí ở \({25^ \circ }{\rm{C}}\) là khí lý tưởng, số mol không khí trong khí cầu ở nhiệt độ \({25^ \circ }{\rm{C}}\) là \(1247,8{\rm{\;mol}}\).

     d) Khi không khí trong khí cầu bị đốt nóng, nó bị giãn nở và một phần bị đẩy ra ngoài thông qua lỗ thoát khí phía trên khí cầu. Biết ở \({25^ \circ }{\rm{C}}\) khối lượng riêng của không khí là \(1,29{\rm{\;kg/}}{{\rm{m}}^3}\), vỏ khí cầu mỏng, không giãn và nhẹ. Để quả cầu rời khỏi mặt đất, nhiệt độ khí trong khí cầu phải đạt tối thiểu là \({64,2^ \circ }{\rm{C}}\).

Phương pháp:

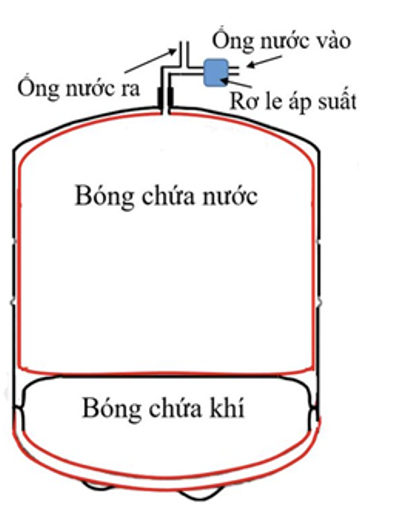
Tổng thể tích của nước và túi khí không đổi

Nhiệt độ của bóng của khí không đổi, áp dụng công thức định luật Boyle: \({p_1}{V_1} = {p_2}{V_2}\)

Cách giải:

a) Khi nước bơm vào bình, thể tích của nước tăng, thể tích của bóng khí giảm, áp suất trong bóng khí tăng

\( \to \) a đúng

b) Bóng khí kín, số phân tử khí không đổi

\( \to \) b sai

c) Khi nước trong bình là 9 lít, thể tích của bóng khí là:

\({V_2} = 12 - 9 = 3\) (lít\()\)

Xét lượng khí trong bóng không đổi

Trạng thái 1 khi bình không chứa nước: \(\left\{ {\begin{array}{*{20}{l}}{{p_1} = 120{\rm{kPa}}}\\{{V_1} = 12{\rm{\;}}lần {\rm{\;}}}\end{array}} \right.\)

Trạng thái 2 khi bình chứa 9 lít nước: \(\left\{ {\begin{array}{*{20}{l}}{{p_2}}\\{{V_2} = 3{\rm{\;}}lần }\end{array}} \right.\)

Áp dụng công thức định luật Boyle, ta có:

\({p_1}{V_1} = {p_2}{V_2} \Rightarrow {p_2} = {p_1}\frac{{{V_1}}}{{{V_2}}} = 120.\frac{{12}}{3} = 480\left( {{\rm{kPa}}} \right)\)

\( \to \) c sai

Áp dụng công thức định luật Boyle, ta có:

\({p_1}{V_1} = {p_3}{V_3} \Rightarrow {p_3} = {p_1}\frac{{{V_1}}}{{{V_3}}} = 120.\frac{{12}}{6} = 240\left( {{\rm{kPa}}} \right)\)

Vậy khi áp suất bằng 240 kPa thì rơ le đóng mạch để cung cấp nước trở lại

Xét lượng khí thoát ra có số mol là \({n_2}\), số mol khí ban đầu là \({n_1}\)

Áp dụng phương trình Clapeyron cho khí trước và sau khi xả khi áp suất đạt giá trị 240 kPa :

\({p_3}{V_3} = {n_1}RT\)

\({p_3}{V_4} = {n_2}RT\)

\( \Rightarrow \frac{{{n_2}}}{{{n_1}}} = \frac{{{V_4}}}{{{V_3}}} = \frac{{12 - 7,2}}{6} = 0,8\)

\( \Rightarrow {\rm{\Delta }}n = {n_1} - {n_2} = 0,2{n_1} = {n_1}.20{\rm{\% }}\)

\( \to \) d đúng

Phương pháp:

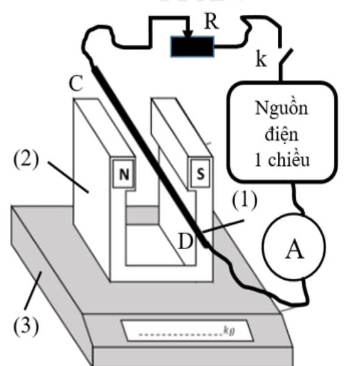
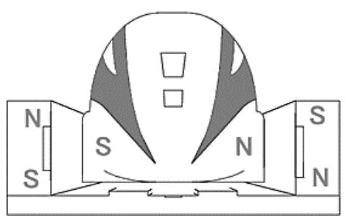
Định luật III Newton: lực do từ trường của nam châm tác dụng lực từ lên dây dẫn có dòng điện chạy qua, thì dây dẫn cũng tác dụng lên nam châm một lực từ cùng phương, ngược chiều, cùng độ lớn với lực từ tác dụng lên dây dẫn

Quy tắc bàn tay trái: đặt bàn tay trái sao cho các đường sức từ hướng vào lòng bàn tay, chiều từ cổ tay đến ngón tay giữa là chiều dòng điện thì ngón tay cái choãi ra \({90^ \circ }\) chỉ chiều của lực từ tác dụng lên dây dẫn

Độ lớn lực từ: \(F = IBl{\rm{sin}}\alpha \)

Cách giải:

a) Số chỉ của cân tăng lên chứng tỏ có một lực tác dụng lên nam châm theo phương thẳng đứng, chiều hướng xuống \( \to \) a đúng

b) Độ lớn lực từ tác dụng lên dây dẫn bằng trọng lượng của vật có khối lượng hiển thị trên cân

\( \to \) b sai

c) Lực từ do dây dẫn tác dụng lên nam châm có chiều hướng xuống \( \to \) lực từ tác dụng lên dây dẫn có chiều hướng lên

Áp dụng quy tắc bàn tay trái: \(\vec F\) hướng lên, \(\vec B\) hướng từ trái sang phải \( \to \) cường độ dòng điện có chiều từ C đến D

\( \to \) c sai

d) Độ lớn lực từ tác dụng lên dây dẫn bằng trọng lượng của vật có khối lượng hiển thị trên cân:

\(F = IBl = mg \Rightarrow B = \frac{{mg}}{{Il}}\)

Cảm ứng từ trong các lần đo tương ứng là:

\({B_1} = \frac{{{m_1}g}}{{{I_1}l}} = \frac{{{{4,1.10}^{ - 3}}.9,8}}{{2,51.0,1}} \approx 0,1601\left( T \right)\)

\({B_2} = \frac{{{m_2}g}}{{{I_2}l}} = \frac{{{{5,31.10}^{ - 3}}.9,8}}{{3,22.0,1}} \approx 0,1616\left( T \right)\)

\({B_3} = \frac{{{m_3}g}}{{{I_3}l}} = \frac{{{{7,15.10}^{ - 3}}.9,8}}{{4,36.0,1}} \approx 0,1607\left( T \right)\)

\({B_4} = \frac{{{m_4}g}}{{{I_4}l}} = \frac{{{{8,16.10}^{ - 3}}.9,8}}{{5,02.0,1}} \approx 0,1593\left( T \right)\)

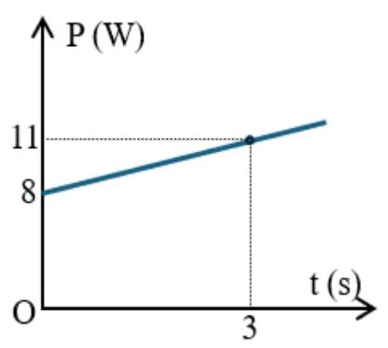
\({B_5} = \frac{{{m_5}g}}{{{I_5}l}} = \frac{{{{11.10}^{ - 3}}.9,8}}{{6,74.0,1}} \approx 0,1599\left( T \right)\)

Giá trị trung bình của cảm ứng từ là:

\(\overline B  = \frac{{0,1601 + 0,1616 + 0,1607 + 0,1593 + 0,1599}}{5} \approx 0,16032\left( T \right)\)