Biểu diễn mẫu số liệu ghép nhóm về cân nặng (đơn vị: kilogam) của 40 học sinh một lớp 12 ở một trường trung học phổ thông được cho dưới bảng sau.

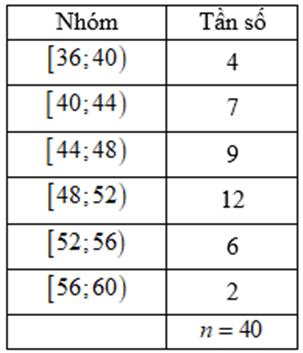
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là

Cho bảng thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2024 của bác An và bác Bình. Gọi R_A, R_B lần lượt là khoảng biến thiên của mẫu số liệu về thời gian tập thể dục của bác An và bác Bình. Khi đó R_A + R_B bằng

Khảo sát thời gian đọc sách trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

\(\left[ {0\,;30} \right)\)

Tính khoảng tứ phân vị của mẫu số liệu.

Thống kê thu nhập theo tháng (đơn vị: triệu đồng) của một nhóm người chạy Grab được cho trong bảng sau:

(a) Cỡ mẫu n = 22.

(b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là Q₁ = 10.

(c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q₃ = 5.

(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là _Q = 5.

Thời gian chờ khám bệnh của hai phòng khám 1 và phòng khám 2 ở thành phố X được cho trong bảng sau:

(a) Tổng số bệnh nhân chờ khám bệnh ở phòng khám số 1 dưới 5 phút là 3.

(b) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian chờ khám bệnh của phóng khám số 1 là R₁ = 15.

(c) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian chờ khám bệnh của phòng khám số 2 là R₂ = 20.

(d) Thời gian chờ khám bệnh ở phòng khám số 2 phân tán hơn thời gian chờ khám bệnh ở phòng khám số 1.

Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:

Tính khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả cuối cùng đến hàng phần mười không làm tròn các kết quả trung gian).

Bảng sau thống kê cân nặng của 30 quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là

Bảng sau biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng)

(a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[R = 30\].

(b) Số phần tử của mẫu là \[n = 60\].

(c) Tứ phân vị thứ nhất là \[{Q_1} = 15\].

(d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[{\Delta _Q} = 3\].