Để có một cốc nước trà giải khát, người ta bỏ 200 g nước đá ở vào một cốc chứa 200 g nước trà ở . Cho nhiệt nóng chảy riêng của nước đá bằng \({3,36.10^5}\;{\rm{J}}/{\rm{kg}}\), nhiệt dung riêng của nước trà bằng \(4200\;{\rm{J}}/({\rm{kg}}\). K). Coi rằng chỉ có sự trao đổi nhiệt giữa nước trà và nước đá. Khi xảy ra sự cân bằng nhiệt thì trong cốc
A. còn 100 g nước đá.
B. còn 150 g nước đá
Quảng cáo
Trả lời:
}{\rm{C}}\) là \({Q_n} = {m_n}c{t_n} = 0,2.4200.60 = 50400\;{\rm{J}}\)
Nhiệt nóng chảy nước đá hoàn toàn là \({Q_{nc}} = {m_d}\lambda = {0,2.3,36.10^5} = 67200\;{\rm{J}}\)
Vì \({Q_n} < {Q_d}\) nên nước đá không tan hết và nhiệt độ cân bằng là
Khối lượng nước đá nóng chảy là \({m_d}^\prime = \frac{{{Q_n}}}{\lambda } = \frac{{50400}}{{{{3,36.10}^5}}} = 0,15\;{\rm{kg}} = 150\;{\rm{g}}\)
Khối lượng nước đá còn lại là \({m_d} - {m_d}^\prime = 200 - 150 = 50\;{\rm{g}}\). Chọn D
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
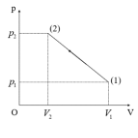
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{p_1} = a{V_1} + b}\\{{p_2} = a{V_2} + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = a.30 + b}\\{15 = a.10 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 0,5}\\{b = 20}\end{array} \to p = - 0,5V + 20} \right.} \right.} \right.\)
\(\frac{{pV}}{T} = {\rm{ const }} \Rightarrow {T_{\max }}{\rm{ khi }}{(pV)_{\max }}\)
\(pV = - 0,5{V^2} + 20V\) đạo hàm được \( - V + 20 = 0 \Rightarrow V = 20{\rm{ lít}} \Rightarrow {(pV)_{\max }} = 200\)
\(\frac{{{W_{d\max }}}}{{{W_{d\min }}}} = \frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{{{(pV)}_{\max }}}}{{{{(pV)}_{\min }}}} = \frac{{200}}{{150}} = \frac{4}{3} \approx 1,3\)
Trả lời ngắn: 1,3
Lời giải
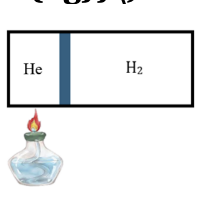
Khi pit-tông dịch chuyển đến chính giữa của xilanh thì p và V ở 2 phần bằng nhau
Trả lời ngắn: 327
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.