Một nhóm học sinh làm thí nghiệm để xác định nhiệt hóa hơi riêng của nước như sau: nối oát kế với một ấm siêu tốc chứa nước, đặt ấm lên một cân điện tử, cấp điện cho ấm siêu tốc; khi nước đã sôi nhóm học sinh mở nắp ấm để hơi nước thoát ra, và ghi lại số chi của oát kế, của cân theo thời gian thì thu được bảng số liệu sau:
Thời gian (phút)
0
1
2
3
Số chỉ oát kế (W)
1003
997
1001
999
Số chỉ cân (gam)
2500
2318
2138
1960
a) Công suất trung bình của ấm điện bằng 1000 W.
b) Lượng hơi nước thoát ra trong 3 phút khảo sát bằng 540 g.
c) Trong khoảng thời gian nước sôi, nhiệt độ của nước liên tục tăng.
d) Coi rằng mất mát nhiệt ra môi trường không đáng kể, từ bảng số liệu trên nhóm học sinh tính toán được nhiệt hóa hơi riêng của nước trong thí nghiệm bằng \({3,3.10^5}\;{\rm{J}}/{\rm{kg}}\) (làm tròn kết quả đến chữ số hàng phần mười).
Một nhóm học sinh làm thí nghiệm để xác định nhiệt hóa hơi riêng của nước như sau: nối oát kế với một ấm siêu tốc chứa nước, đặt ấm lên một cân điện tử, cấp điện cho ấm siêu tốc; khi nước đã sôi nhóm học sinh mở nắp ấm để hơi nước thoát ra, và ghi lại số chi của oát kế, của cân theo thời gian thì thu được bảng số liệu sau:
|
Thời gian (phút) |
0 |
1 |
2 |
3 |
|
Số chỉ oát kế (W) |
1003 |
997 |
1001 |
999 |
|
Số chỉ cân (gam) |
2500 |
2318 |
2138 |
1960 |
a) Công suất trung bình của ấm điện bằng 1000 W.
b) Lượng hơi nước thoát ra trong 3 phút khảo sát bằng 540 g.
c) Trong khoảng thời gian nước sôi, nhiệt độ của nước liên tục tăng.
d) Coi rằng mất mát nhiệt ra môi trường không đáng kể, từ bảng số liệu trên nhóm học sinh tính toán được nhiệt hóa hơi riêng của nước trong thí nghiệm bằng \({3,3.10^5}\;{\rm{J}}/{\rm{kg}}\) (làm tròn kết quả đến chữ số hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(\bar P = \frac{{{P_1} + {P_2} + {P_3} + {P_4}}}{4} = \frac{{1003 + 997 + 1001 + 999}}{4} = 1000\;{\rm{W}} \Rightarrow \)a) Đúng
Lượng hơi nước thoát ra trong 3 phút khảo sát bằng \(5\Delta m = 2500 - 1960 = 540\;{\rm{g}} \Rightarrow \) b) Đúng Trong khoảng thời gian nước sôi, nhiệt độ của nước không đổi \( \Rightarrow \) c) Sai
\(L = \frac{Q}{{\Delta m}} = \frac{{Pt}}{{\Delta m}} = \frac{{1000 \cdot 3 \cdot 60}}{{0,54}} \approx 3,3 \cdot {10^5}\;{\rm{J}}/{\rm{kg}} \Rightarrow \) d) Đúng
Chú ý: Giá trị nhiệt hóa hơi riêng bị sai số khá lớn so với thực tế
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
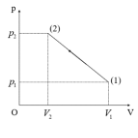
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{p_1} = a{V_1} + b}\\{{p_2} = a{V_2} + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = a.30 + b}\\{15 = a.10 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 0,5}\\{b = 20}\end{array} \to p = - 0,5V + 20} \right.} \right.} \right.\)
\(\frac{{pV}}{T} = {\rm{ const }} \Rightarrow {T_{\max }}{\rm{ khi }}{(pV)_{\max }}\)
\(pV = - 0,5{V^2} + 20V\) đạo hàm được \( - V + 20 = 0 \Rightarrow V = 20{\rm{ lít}} \Rightarrow {(pV)_{\max }} = 200\)
\(\frac{{{W_{d\max }}}}{{{W_{d\min }}}} = \frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{{{(pV)}_{\max }}}}{{{{(pV)}_{\min }}}} = \frac{{200}}{{150}} = \frac{4}{3} \approx 1,3\)
Trả lời ngắn: 1,3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
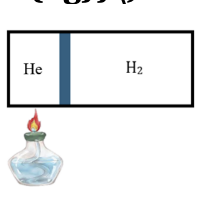
Khi pit-tông dịch chuyển đến chính giữa của xilanh thì p và V ở 2 phần bằng nhau
Trả lời ngắn: 327
Câu 3
A. còn 100 g nước đá.
B. còn 150 g nước đá
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập