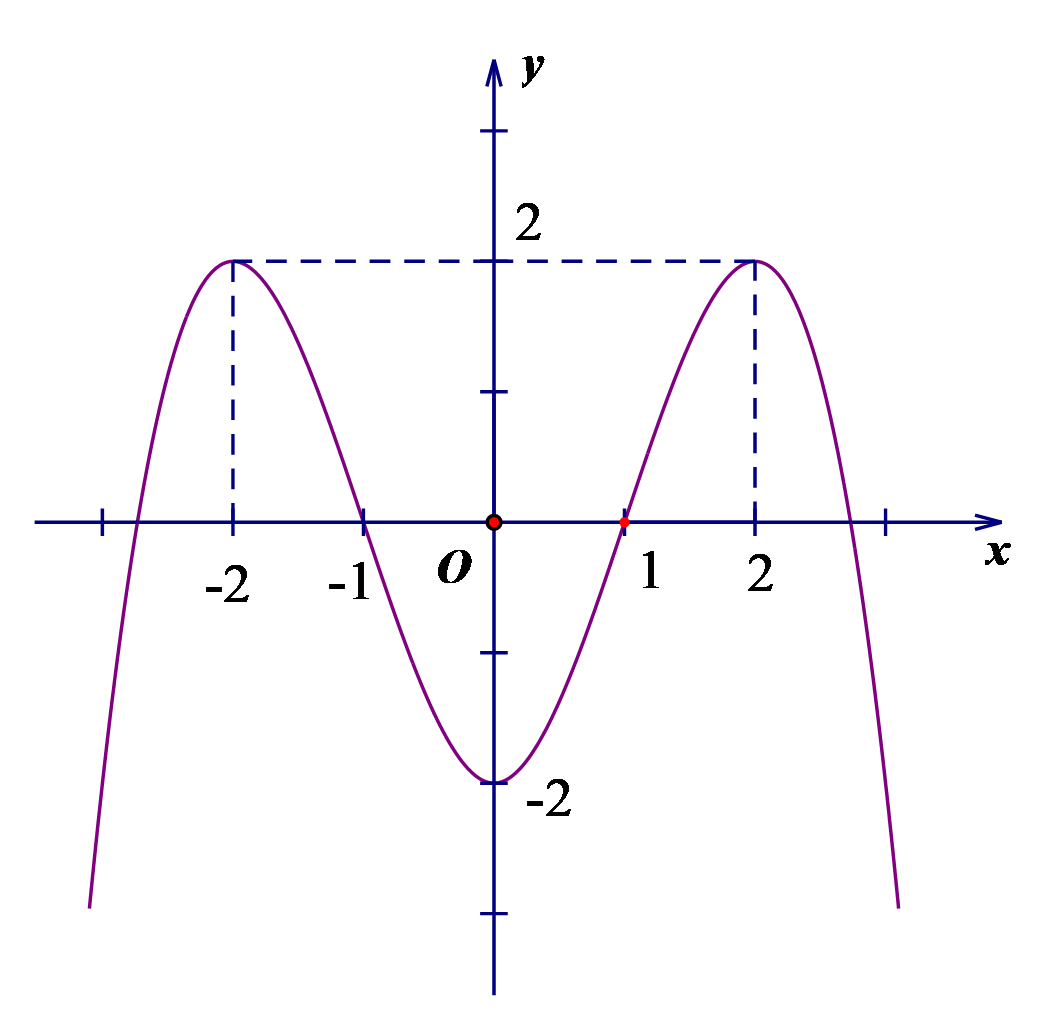
Tìm khoảng nghịch biến của hàm số: \[y = \frac{{3 - 2x}}{{x + 7}}\].
Quảng cáo
Trả lời:
Hàm số đã cho xác định và liên tục trên: \[{\rm{D}} = \mathbb{R}\backslash \left\{ { - 7} \right\}\].
Tính\[y' = \frac{{\left( { - 2} \right).7 - 1.3}}{{{{\left( {x + 7} \right)}^2}}} = \frac{{ - 17}}{{{{\left( {x + 7} \right)}^2}}} < 0,\forall x \in {\rm{D}} = \mathbb{R}\backslash \left\{ { - 7} \right\}\].
Bảng biến thiên:
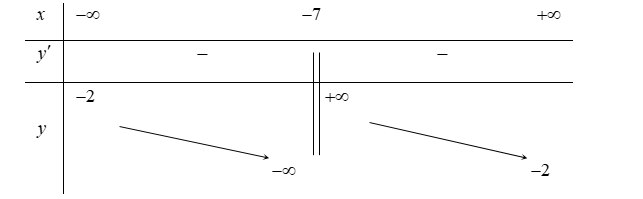
Hàm số đã cho luôn nghịch biến trên: \[\left( { - \infty ; - 7} \right)\] và \[\left( { - 7; + \infty } \right)\]. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
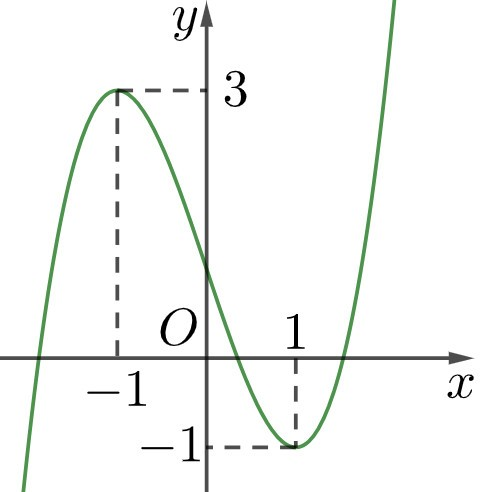
a) Hàm số \(y = f(x)\) đồng biến trên các khoảng \(( - \infty ; - 1)\) và \((1; + \infty ).\)
b) Giá trị cực đại là y = 3, giá trị cực tiểu là y = –1.
Do đó tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho là 3 – 1 = 2.
c) Hàm số \(y = f(x)\)có hai cực trị là \(x = \pm 1.\)
d) Gọi \[d:y = ax + b\] là đường thẳng qua hai điểm cực trị \[A( - 1;3),B(1; - 1).\]
\[A,B \in d \Rightarrow \left\{ \begin{array}{l} - a + b = 3\\a + b = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 1\end{array} \right. \Rightarrow d:y = - 2x + 1\].
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Lời giải
Có \(N'\left( t \right) = \frac{{100\left( {100 + {t^2}} \right) - 200{t^2}}}{{{{\left( {100 + {t^2}} \right)}^2}}}\)\( = \frac{{{{100}^2} - 100{t^2}}}{{{{\left( {100 + {t^2}} \right)}^2}}}\);
\(N'\left( t \right) = 0 \Leftrightarrow t = 10\) (vì t > 0).
Ta có bảng biến thiên
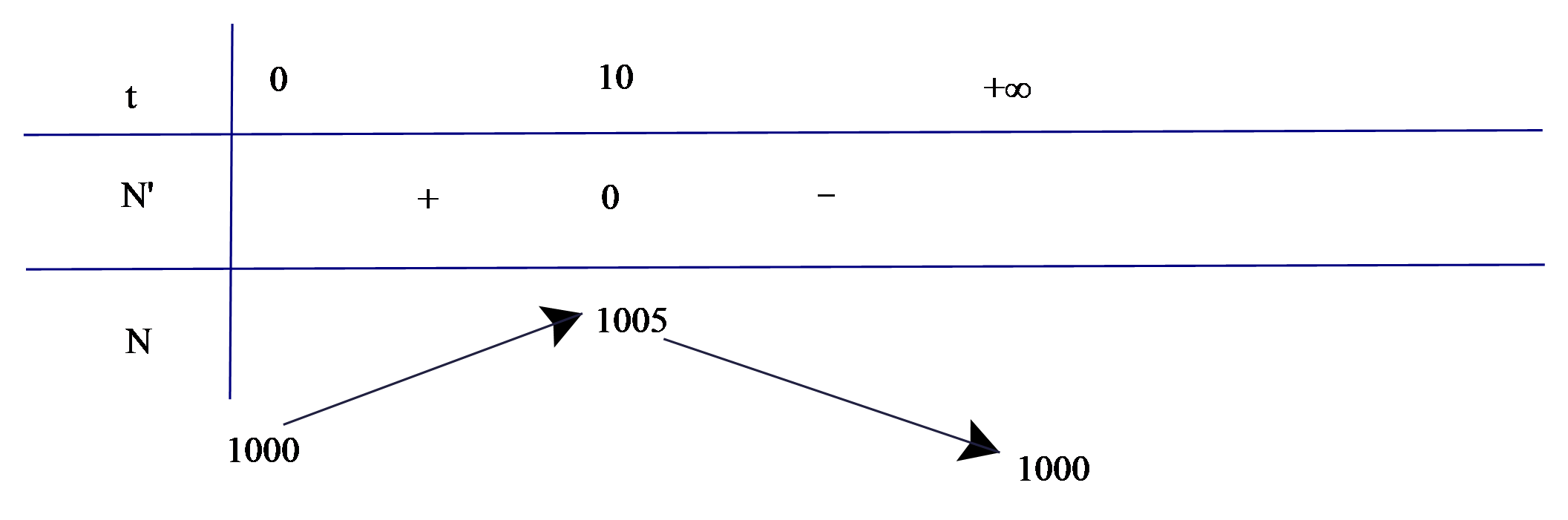
Dựa vào bảng biến thiên, ta có số lượng vi khuẩn đạt cực đại khi t = 10 giây.
Trả lời: 10.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.