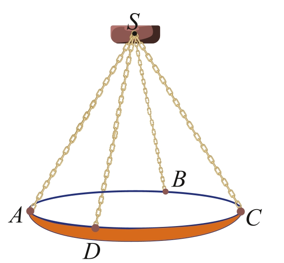
Có hai xã \(A,\,B\) cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là \(AA' = 550\)m, \(BB' = 600\)m. Người ta đo được \(A'B' = 2200\)m như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm cạnh bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí \(M\) của trạm cung cấp nước sạch đó trên đoạn \(A'B'\) sao cho tổng khoảng cách từ hai xã đến vị trí \(M\) là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
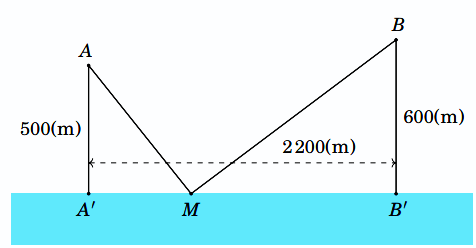
Có hai xã \(A,\,B\) cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là \(AA' = 550\)m, \(BB' = 600\)m. Người ta đo được \(A'B' = 2200\)m như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm cạnh bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí \(M\) của trạm cung cấp nước sạch đó trên đoạn \(A'B'\) sao cho tổng khoảng cách từ hai xã đến vị trí \(M\) là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.

Quảng cáo
Trả lời:
Đặt \(A'M = x\,\,\left( {0 < x < 2200} \right)\), \(B'M = 2200 - x\)
Ta có \(AM = \sqrt {{x^2} + {{500}^2}} \,,\,\,BM = \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \)
Khi đó tổng khoảng cách từ hai xã đến vị trí \(M\) là:
\(AM + BM = \sqrt {{x^2} + {{500}^2}} \, + \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \)
Xét hàm số \(f\left( x \right) = \sqrt {{x^2} + {{500}^2}} \, + \sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} \) trên khoảng \(\left( {0;\,2200} \right)\)
Đạo hàm \(f'\left( x \right) = \frac{x}{{\sqrt {{x^2} + {{500}^2}} }} - \frac{{2200 - x}}{{\sqrt {{{\left( {2200 - x} \right)}^2} + {{600}^2}} }} = 0 \Leftrightarrow x = 1000\)
Bảng biến thiên:
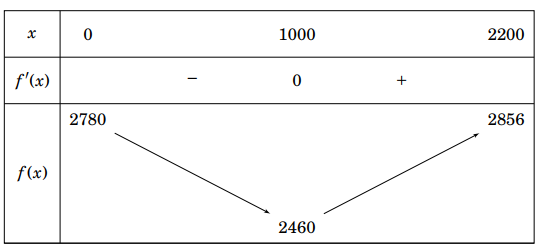
Vậy giá trị nhỏ nhất của tổng khoảng cách từ hai xã đó đến bờ sông là khoảng \(2460\)m, tại vị trí \(M\) cách điểm \(A'\) là \(1000\)m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (triệu VNĐ) là số tiền cần giảm cho mỗi chiếc xe\[\left( {0 \le x \le 4} \right).\]
Số lượng xe bán ra được trong một năm sau khi giảm giá là: \[x.200 + 600\](chiếc)
Số lợi nhuận thu được từ việc bán xe trong một năm sau khi giảm giá là: \[\left( {x.200 + 600} \right)\left( {4 - x} \right)\]
Xét hàm số \[f\left( x \right) = \left( {x.200 + 600} \right)\left( {4 - x} \right) = 200\left( { - {x^2} + x + 12} \right)\,\,\,\left( {0 \le x \le 4} \right)\].
Có \(f'\left( x \right) = 200\left( { - 2x + 1} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow - 2x + 1 = 0 \Leftrightarrow x = \frac{1}{2}\).
Có \(f\left( 0 \right) = 2400;f\left( {\frac{1}{2}} \right) = 2450;f\left( 4 \right) = 0\).
Lời giải
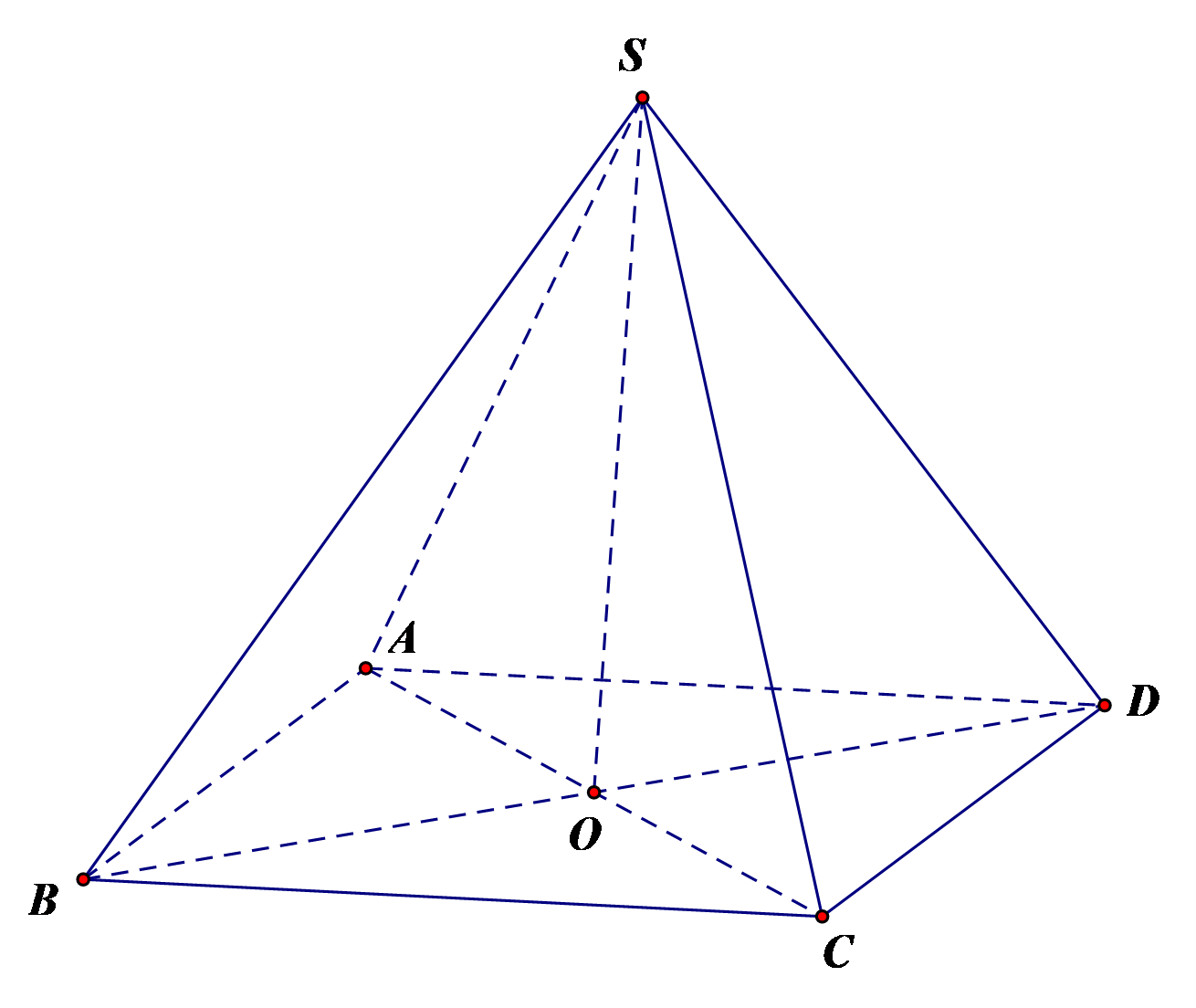
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ không đồng phẳng.
Vì 5 điểm S, A, B, C, D không cùng thuộc 1 mặt phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|\) .
c) Độ lớn trọng lực tác động lên đèn chùm là: \(P = mg = 5.10 = 50\;N\).
d) Ta có \(S.ABCD\) là hình chóp tứ giác đều. Suy ra \(SA = SB = SC = SD\) mà \(\widehat {ASC} = 60^\circ \).
Vậy tam giác \[SAC\] đều. Gọi \[O\] là trung điểm \(AC\).
Hợp lực của 4 sợi xích là: \(\vec F = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \)
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay \(4\overrightarrow {SO} = \vec P\) hay \(4SO = P \Leftrightarrow SO = 12,5\).
Xét tam giác đều \(SAC\)có \(SA = \frac{2}{{\sqrt 3 }}SO = \frac{{25\sqrt 3 }}{3}\).
Vậy độ lớn của lực căng cho mỗi sợi xích là \(\frac{{25\sqrt 3 }}{3}\;N\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.