Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1km theo đường chim bay và chiến sỹ cách bờ bên kia 100m.
Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1km theo đường chim bay và chiến sỹ cách bờ bên kia 100m.
Quảng cáo
Trả lời:
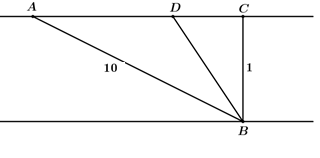
Gọi \(A\) là mục tiêu; \(B\) là vị trí chiến sỹ và \(BD\) là đường bơi của chiến sỹ.
Chọn một đơn vị độ dài là 100 m suy ra \[BC = 1;AB = 10;\]\[AC = 3\sqrt {11} \].
Gọi vận tốc bơi của chiến sỹ là một đơn vị vận tốc thì vận tốc chạy của chiến sỹ là 3 đơn vị vận tốc. Gọi \(x\) là quãng đường chiến sỹ bơi suy ra \(BD = x\)
Vậy quãng đường chiến sỹ chạy là \[AD = AC - CD = 3\sqrt {11} - \sqrt {{x^2} - 1} \].
Thời gian chiến sỹ đến được mục tiêu là: \[t = \frac{{3\sqrt {11} - \sqrt {{x^2} - 1} }}{3} + \frac{x}{1} = \sqrt {11} - \frac{1}{3}\sqrt {{x^2} - 1} + x\]
Xét hàm \[f\left( x \right) = \sqrt {11} - \frac{1}{3}\sqrt {{x^2} - 1} + x\] có \[f'\left( x \right) = 1 - \frac{1}{3}\frac{x}{{\sqrt {{x^2} - 1} }} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\sqrt 2 }}{4}\left( {tm} \right)\\x = - \frac{{3\sqrt 2 }}{4}\left( {ktm} \right)\end{array} \right.\].
Bảng biến thiên:
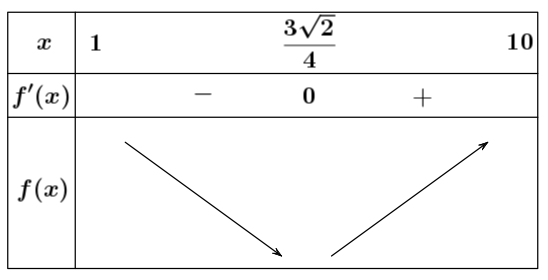
Vậy thời gian chiến sỹ đến mục tiêu ngắn nhất khi \[f{\left( x \right)_{\min }} \Rightarrow x = \frac{{3\sqrt 2 }}{4}\]
Vậy chiến sỹ phải bơi \[\frac{{3\sqrt 2 }}{4}.100 = 75\sqrt 2 \left( {\rm{m}} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (triệu VNĐ) là số tiền cần giảm cho mỗi chiếc xe\[\left( {0 \le x \le 4} \right).\]
Số lượng xe bán ra được trong một năm sau khi giảm giá là: \[x.200 + 600\](chiếc)
Số lợi nhuận thu được từ việc bán xe trong một năm sau khi giảm giá là: \[\left( {x.200 + 600} \right)\left( {4 - x} \right)\]
Xét hàm số \[f\left( x \right) = \left( {x.200 + 600} \right)\left( {4 - x} \right) = 200\left( { - {x^2} + x + 12} \right)\,\,\,\left( {0 \le x \le 4} \right)\].
Có \(f'\left( x \right) = 200\left( { - 2x + 1} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow - 2x + 1 = 0 \Leftrightarrow x = \frac{1}{2}\).
Có \(f\left( 0 \right) = 2400;f\left( {\frac{1}{2}} \right) = 2450;f\left( 4 \right) = 0\).
Lời giải
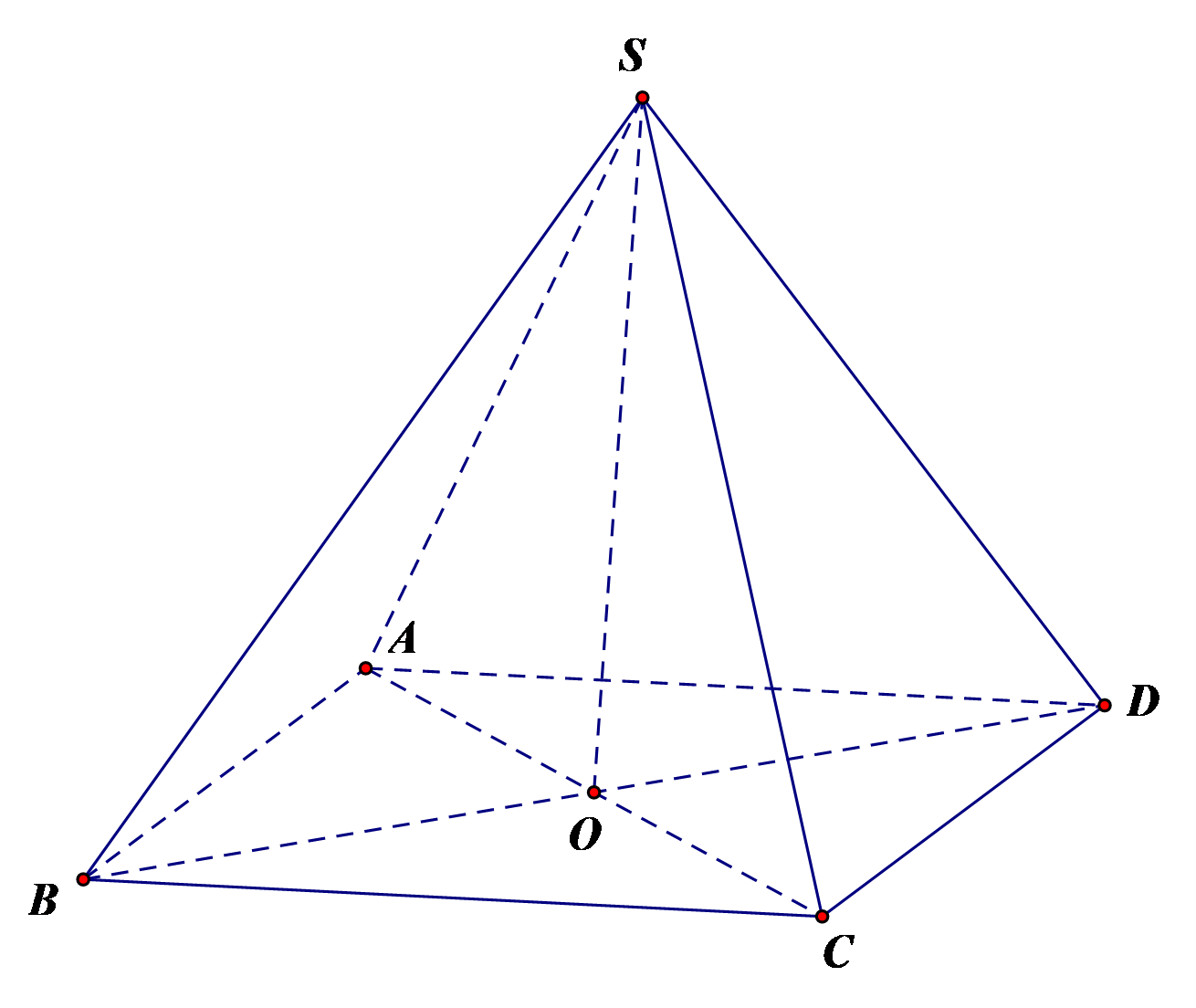
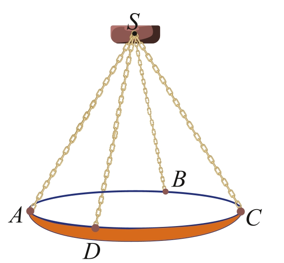
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ không đồng phẳng.
Vì 5 điểm S, A, B, C, D không cùng thuộc 1 mặt phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|\) .
c) Độ lớn trọng lực tác động lên đèn chùm là: \(P = mg = 5.10 = 50\;N\).
d) Ta có \(S.ABCD\) là hình chóp tứ giác đều. Suy ra \(SA = SB = SC = SD\) mà \(\widehat {ASC} = 60^\circ \).
Vậy tam giác \[SAC\] đều. Gọi \[O\] là trung điểm \(AC\).
Hợp lực của 4 sợi xích là: \(\vec F = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \)
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay \(4\overrightarrow {SO} = \vec P\) hay \(4SO = P \Leftrightarrow SO = 12,5\).
Xét tam giác đều \(SAC\)có \(SA = \frac{2}{{\sqrt 3 }}SO = \frac{{25\sqrt 3 }}{3}\).
Vậy độ lớn của lực căng cho mỗi sợi xích là \(\frac{{25\sqrt 3 }}{3}\;N\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.