Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.

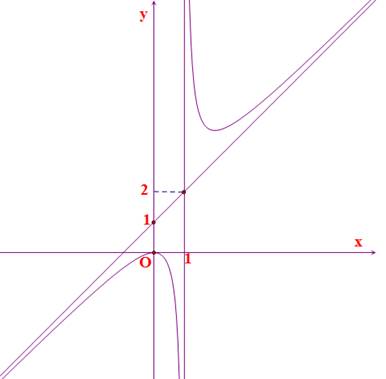
Ta có \(y = ax + b\) là đường tiệm cận xiên của đồ thị hàm số.

Từ đồ thị ta suy ra được \(y = x + 1\) là tiệm cận xiên nên \(a = 1,b = 1\)

\(x = 1\) là tiệm cận đứng của đồ thị hàm số nên \(c = - 1\)

Vậy \(a + b + c = 1\).

Trả lời: 1.

Với \(m = 1\), hàm số có dạng \(y = \frac{{{x^2} + x - 2}}{{x + 3}} = x - 2 + \frac{4}{{x + 3}}\).

a) Ta có \(y' = 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}}\); \(y' = 0 \Leftrightarrow 1 - \frac{4}{{{{\left( {x + 3} \right)}^2}}} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\).

Bảng biến thiên

Dựa vào bảng biến thiên, hàm số có 2 điểm cực trị.

b) Có \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 2} \right)} \right] = 0\) nên \(y = x - 2\) là tiệm cận xiên của đồ thị hàm số.

c) \(\mathop {\lim }\limits_{x \to - {3^ + }} \frac{{{x^2} + x - 2}}{{x + 3}} = + \infty \); \(\mathop {\lim }\limits_{x \to - {3^ - }} \frac{{{x^2} + x - 2}}{{x + 3}} = - \infty \) nên \(x = - 3\) là tiệm cận đứng của đồ thị hàm số.

Thay \(x = - 3\) vào \(y = x - 2\) được \(y = 1\).

Do đó giao điểm của tiệm cận đứng và tiệm cận xiên là \(I\left( { - 3;1} \right)\).

d) Ta có: \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}} = mx - 2 + \frac{{6m - 2}}{{x + 3m}}\)

* Nếu \(m = \frac{1}{3}\) đồ thị hàm số không tồn tại hai tiệm cận

* Nếu \(m \ne \frac{1}{3}\), đồ thị hàm số có hai tiệm cận

\({d_1}:x = - 3m \Leftrightarrow x + 3m = 0\) và \({d_2}:y = mx - 2 \Leftrightarrow mx - y - 2 = 0\).

\( \Rightarrow \overrightarrow {{n_1}} (1;0),{\rm{ }}\overrightarrow {{n_2}} (m; - 1)\) lần lượt là vectơ pháp tuyến của \({d_1}\) và \({d_2}\).

Góc giữa \({d_1}\) và \({d_2}\) bằng \(45^\circ \Leftrightarrow \cos 45^\circ = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\)\( \Leftrightarrow \frac{{\left| m \right|}}{{\sqrt {{m^2} + 1} }} = \frac{{\sqrt 2 }}{2} \Leftrightarrow m = \pm 1\).

Đáp án: a) Đúng;   b) Đúng;   c) Sai; d) Đúng.