Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình \[2x-3y = 5?\]
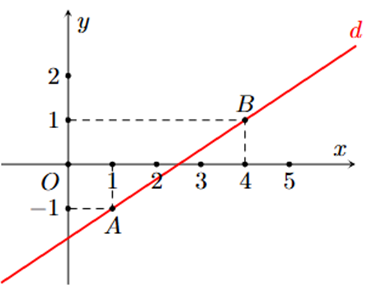
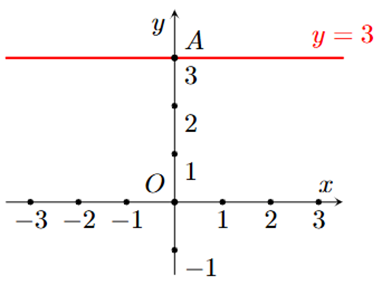
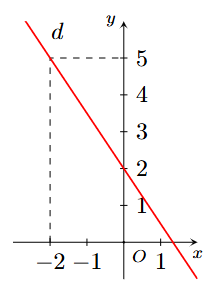
Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình \[2x-3y = 5?\]
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
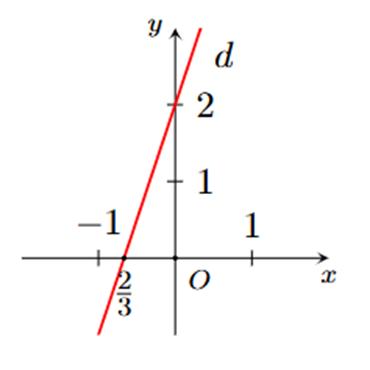
Ta có: \[2x-3y = 5\] suy ra \(y = \frac{2}{3}x - \frac{5}{3}.\)
Do đó, tất cả các nghiệm của phương trình \[2x-3y = 5\] được biểu diễn trên đường thẳng \(y = \frac{2}{3}x - \frac{5}{3}.\)
• Cho \[x = 1\] thì \[y = - 1,\] do đó đường thẳng đi qua điểm có tọa độ \[\left( {1\,;\,\, - 1} \right).\]
• Cho \[x = 4\] thì \[y = 1,\] do đó đường thẳng đi qua điểm có tọa độ \[\left( {4\,;\,\,1} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: 4.
Điều kiện xác định: \(x \ne 2,\,\,\,x \ne - 2.\)
\(\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{2 + x}} = \frac{{{x^2} + 16}}{{{x^2} - 4}}\)
\(\frac{{{{\left( {x + 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{{x^2} + 16}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\({\left( {x + 2} \right)^2} - {\left( {x - 2} \right)^2} = {x^2} + 16\)
\({x^2} + 4x + 4 - \left( {{x^2} - 4x + 4} \right) = {x^2} + 16\)
\({x^2} + 4x + 4 - {x^2} + 4x - 4 = {x^2} + 16\)
\({x^2} - 8x + 16 = 0\)
\({\left( {x - 4} \right)^2} = 0\)
\(x - 4 = 0\)
\(x = 4\) (thỏa mãn).
Vậy nghiệm của phương trình đã cho là \(x = 4\).
Lời giải
Hướng dẫn giải
Đáp án: 6.
Ta có \(1 + \frac{{x + 4}}{5} \le x - \frac{{x + 3}}{3}\)
\(\frac{{5 + x + 4}}{5} \le \frac{{3x - x - 3}}{3}\)
\(\frac{{x + 9}}{5} \le \frac{{2x - 3}}{3}\)
\[3\left( {x + 9} \right) \le 5\left( {2x - 3} \right)\]
\[3x + 27 \le 10x - 15\]
\[10x - 3x \le 27 + 15\]
\[7x \ge 42\]
\[x \ge 6\]
Vậy nghiệm của bất phương trình là \[x \ge 6.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.