Cho tam giác \(ABC\) có \(M,\;N\) lần lượt là trung điểm của \(AC,\;BC.\) Gọi \(I\) là giao điểm của \(AN\) và \(BM.\) Trên tia đối của tia \(MB\) lấy điểm \(F\) sao cho \(M\) là trung điểm của \(FI.\) Trên tia đối của tia \(NA\) lấy điểm \(E\) sao cho \(N\) là trung điểm của \(EI.\) Khi đó, \(\widehat F = ...\widehat {ABM}.\) Tìm số thích hợp điền vào dấu “…”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(1\)
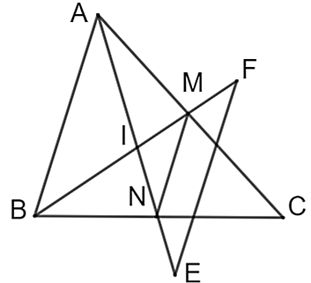
\(\Delta ABC\) có: \(M,\;N\) lần lượt là trung điểm của \(AC,\;BC\) nên \(MN\) là đường trung bình của \(\Delta ABC.\)
Suy ra: \(MN\;{\rm{//}}\;AB\;\left( 1 \right).\)
\(\Delta IEF\) có: \(M\) là trung điểm của \(FI,\;N\) là trung điểm của \(EI\) nên \(MN\) là đường trung bình của \(\Delta IEF.\) Suy ra: \(MN\;{\rm{//}}\;EF\;\left( 2 \right).\)
Từ \(\left( 1 \right),\;\left( 2 \right)\) ta có: \(EF\;{\rm{//}}\;AB.\) Do đó, \(\widehat F = \widehat {ABM}\) (hai góc ở so le trong).
Vậy số thích hợp điền vào dấu “…” là \(1.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
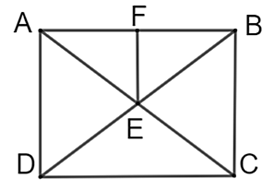
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(E\) là trung điểm của \(BD.\)
\(\Delta ABD\) có: \(E\) là trung điểm của \(BD,\;EF\;{\rm{//}}\;AD\) nên \(F\) là trung điểm của \(AB.\)
\(\Delta ABD\) có: \(E\) là trung điểm của \(BD,\;F\) là trung điểm của \(AB.\)
Do đó, \(EF\) là đường trung bình của \(\Delta ABD.\) Suy ra: \(EF = \frac{1}{2}AD = \frac{1}{2} \cdot 4 = 2\;\left( {{\rm{cm}}} \right).\) Vậy \(EF = 2\;{\rm{cm}}{\rm{.}}\)
Lời giải
Đáp án đúng là: A
Đoạn thẳng nối trung điểm hai cạnh của tam giác là đường trung bình của tam giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo