Cho biểu thức \(B = \left( {\frac{{2x - 1}}{{x + 3}} - \frac{x}{{3 - x}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\) với \(x \ne 3\,;\,\,x \ne - 3\). Hỏi có bao nhiêu giá trị nguyên của \(x\) để \(B\) nhận giá trị nguyên?
Cho biểu thức \(B = \left( {\frac{{2x - 1}}{{x + 3}} - \frac{x}{{3 - x}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\) với \(x \ne 3\,;\,\,x \ne - 3\). Hỏi có bao nhiêu giá trị nguyên của \(x\) để \(B\) nhận giá trị nguyên?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: \(6\).
Với \(x \ne 3\,;\,\,x \ne - 3\), ta có:
\(B = \left( {\frac{{2x - 1}}{{x + 3}} - \frac{x}{{3 - x}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\)
\( = \left[ {\frac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} + \frac{{x\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} - \frac{{3 - 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}}} \right] \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{2{x^2} - 7x + 3 + {x^2} + 3x - 3 + 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3{x^2} + 6x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3x\left( {x + 2} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}} = \frac{{3x}}{{x + 3}}\).
Ta có: \(B = \frac{{3x}}{{x + 3}} = \frac{{3x + 9 - 9}}{{x + 3}} = \frac{{3\left( {x + 3} \right)}}{{x + 3}} - \frac{9}{{x + 3}} = 3 - \frac{9}{{x + 3}}\).
Để \(B\) nguyên thì \(\frac{9}{{x + 3}}\) nhận giá trị nguyên.
Suy ra \(x + 3\) là ước của \(9\).
Mà Ư\(\left( 9 \right) = \left\{ { - 9\,;\,\, - 3\,;\,\, - 1\,;\,\,1\,;\,\,3\,;\,\,9} \right\}\).
Ta có bảng sau:
|
\(x + 3\) |
\( - 9\) |
\( - 3\) |
\( - 1\) |
\(1\) |
\(3\) |
\(9\) |
|
\(x\) |
\( - 12\) (TM) |
\( - 6\) (TM) |
\( - 4\) (TM) |
\( - 2\) (TM) |
\(0\) (TM) |
\(6\) (TM) |
Nhận thấy các giá trị \(x\) tìm được đều thỏa mãn.
Do đó, có 6 giá trị nguyên của \(x\) thỏa mãn yêu cầu bài toán.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 73.
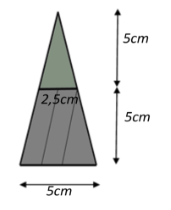
Thể tích của lọ nước hoa hình kim tự tháp là: \[{V_1} = \frac{1}{3} \cdot {5^2} \cdot 10 = \frac{{250}}{3}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\]
Thể tích của nắp lọ nước hoa là: \[{V_2} = \frac{1}{3} \cdot 2,{5^2} \cdot 5 = \frac{{125}}{{12}}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\]
Dung tích của lọ nước hoa đó là: \(\frac{{250}}{3} - \frac{{125}}{{12}} \approx 73\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right) = 73\,\,\left( {{\rm{ml}}} \right)\).
Vậy dung tích của lọ nước hoa đó là \(73\,\,{\rm{ml}}.\)
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
⦁ Ta có \(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy\).
Đa thức \[A\] có bậc là 8. Do đó ý a) đúng.
⦁ Ta có \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}\]
\[ = 12{x^4}{y^5}:\left( {6{x^2}{y^2}} \right) - 36{x^5}{y^4}:\left( {6{x^2}{y^2}} \right) + 6{x^3}{y^3}:\left( {6{x^2}{y^2}} \right)\]
\[ = 2{x^2}{y^3} - 6{x^3}{y^2} + xy\].
Khi đó, hệ số tự do của đa thức \(B\) là 0. Do đó ý b) sai.
⦁ Thay \[x = - 1\,;\,\,y = 1\] vào biểu thức \(B\), ta có:
\[B = 2 \cdot {\left( { - 1} \right)^2} \cdot {1^3} - 6 \cdot {\left( { - 1} \right)^3} \cdot {1^2} + \left( { - 1} \right) \cdot 1 = 2 + 6 - 1 = 7\].
Vậy với \[x = - 1\,;\,\,y = 1\] thì \(B = 7\). Do đó ý c) sai.
⦁ Ta có \(A = M + B\)
Suy ra \(M = A - B\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy - \left( {2{x^2}{y^3} - 6{x^3}{y^2} + xy} \right)\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy - 2{x^2}{y^3} + 6{x^3}{y^2} - xy\)
\( = \left( {2{x^2}{y^3} - 2{x^2}{y^3}} \right) + \left( { - 6{x^3}{y^2} + 6{x^3}{y^2}} \right) + \left( {2xy - xy} \right)\)\( = xy.\)
Như vậy, \(M\) là một đơn thức. Do đó ý d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.