Ghép các dữ liệu với loại dữ liệu thích hợp.
1. Xếp loại mức độ hài lòng của khách hàng: Hài lòng; Khá hài lòng; Chưa hài lòng.
a) Số liệu liên tục.
2. Số nhạc cụ mà năm học sinh trong tổ 1 biết chơi: \(0;\,\,3;\,\,2;\,\,1;\,\,3.\)
b) Số liệu rời rạc.
3. Chiều cao mực nước thủy văn lớn nhất tại sông Tiền trong 5 ngày đầu tháng 8 (đơn vị: mét): \(1,68;\,\,1,75;\,\,1,82;\,\,1,66;\,\,1,62.\)
c) Dữ liệu biểu thị thứ bậc
4. Năm địa điểm du lịch của Việt Nam mà học sinh lớp 8A thích nhất: Vinpearl Safari (Phú Quốc), Đà Lạt, Bà Nà Hill (Đà Nẵng), Đỉnh Fansipan (Sapa – Lào Cai), Vịnh Hạ Long (Quảng Ninh).
d) Dữ liệu định danh
Ghép các dữ liệu với loại dữ liệu thích hợp.
|
1. Xếp loại mức độ hài lòng của khách hàng: Hài lòng; Khá hài lòng; Chưa hài lòng. |
a) Số liệu liên tục. |
|
2. Số nhạc cụ mà năm học sinh trong tổ 1 biết chơi: \(0;\,\,3;\,\,2;\,\,1;\,\,3.\) |
b) Số liệu rời rạc. |
|
3. Chiều cao mực nước thủy văn lớn nhất tại sông Tiền trong 5 ngày đầu tháng 8 (đơn vị: mét): \(1,68;\,\,1,75;\,\,1,82;\,\,1,66;\,\,1,62.\) |
c) Dữ liệu biểu thị thứ bậc |
|
4. Năm địa điểm du lịch của Việt Nam mà học sinh lớp 8A thích nhất: Vinpearl Safari (Phú Quốc), Đà Lạt, Bà Nà Hill (Đà Nẵng), Đỉnh Fansipan (Sapa – Lào Cai), Vịnh Hạ Long (Quảng Ninh). |
d) Dữ liệu định danh |
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1 – c; 2 – b; 3 – a; 4 – d.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
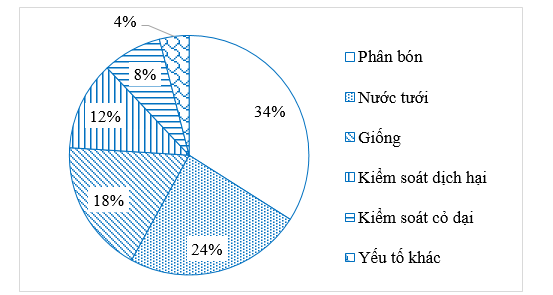
a) Yếu tố Phân bón (chiếm \(34\% )\) ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất.
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì Yếu tố kiểm soát dịch hại gấp số lần Yếu tố khác là: \(\frac{{12\% }}{{4\% }} = 3\) (lần).
c) Một vài biện pháp khắc phục tình trạng vấn đề tưới nước để làm giảm thiệt hại trong việc trồng trọt: khoan thêm giếng, lắp đặt thêm ống dẫn nước từ các hồ chứa, xây dựng phương án tưới cho phù hợp với từng loại cây trồng, áp dụng phương pháp tưới tiết kiệm nước theo hình thức khô – nước xen kẽ, chỉ vô nước giai đoạn bón phân.
Lời giải
Hướng dẫn giải
b) Ta có: \(B = \frac{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}},\) xét phân thức nghịch đảo của phân thức \(B\) là:
\(\frac{1}{B} = \frac{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{26}} + {x^{22}} + {x^{18}} + ... + {x^6} + {x^2}} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{{x^2}\left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{24}} + {x^{20}} + ... + 1} \right)\left( {{x^2} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}} = {x^2} + 1.\)
Vậy \(B = \frac{1}{{{x^2} + 1}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập