Cho hình bên. Biết rằng các số trên hình có cùng đơn vị đo là \({\rm{cm}}.\) Giá trị \(x\) và \(y\) lần lượt là


Quảng cáo
Trả lời:
Đáp án đúng là: D
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của \[\widehat {BAC}\] nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) (tính chất đường phân giác).
Suy ra \(\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}}\) (tính chất tỉ lệ thức).
Theo tính chất của dãy tỉ số bằng nhau ta có:
\[\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}} = \frac{{DC + DB}}{{AC + AB}} = \frac{{BC}}{{AC + AB}} = \frac{{28}}{{15 + 20}} = \frac{4}{5}.\]
Do đó \[\frac{x}{{15}} = \frac{y}{{20}} = \frac{4}{5}\], suy ra \[x = 15 \cdot \frac{4}{5} = 12{\rm{\;(cm),}}\,\,y = 20 \cdot \frac{4}{5} = 16{\rm{\;(cm)}}{\rm{.}}\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
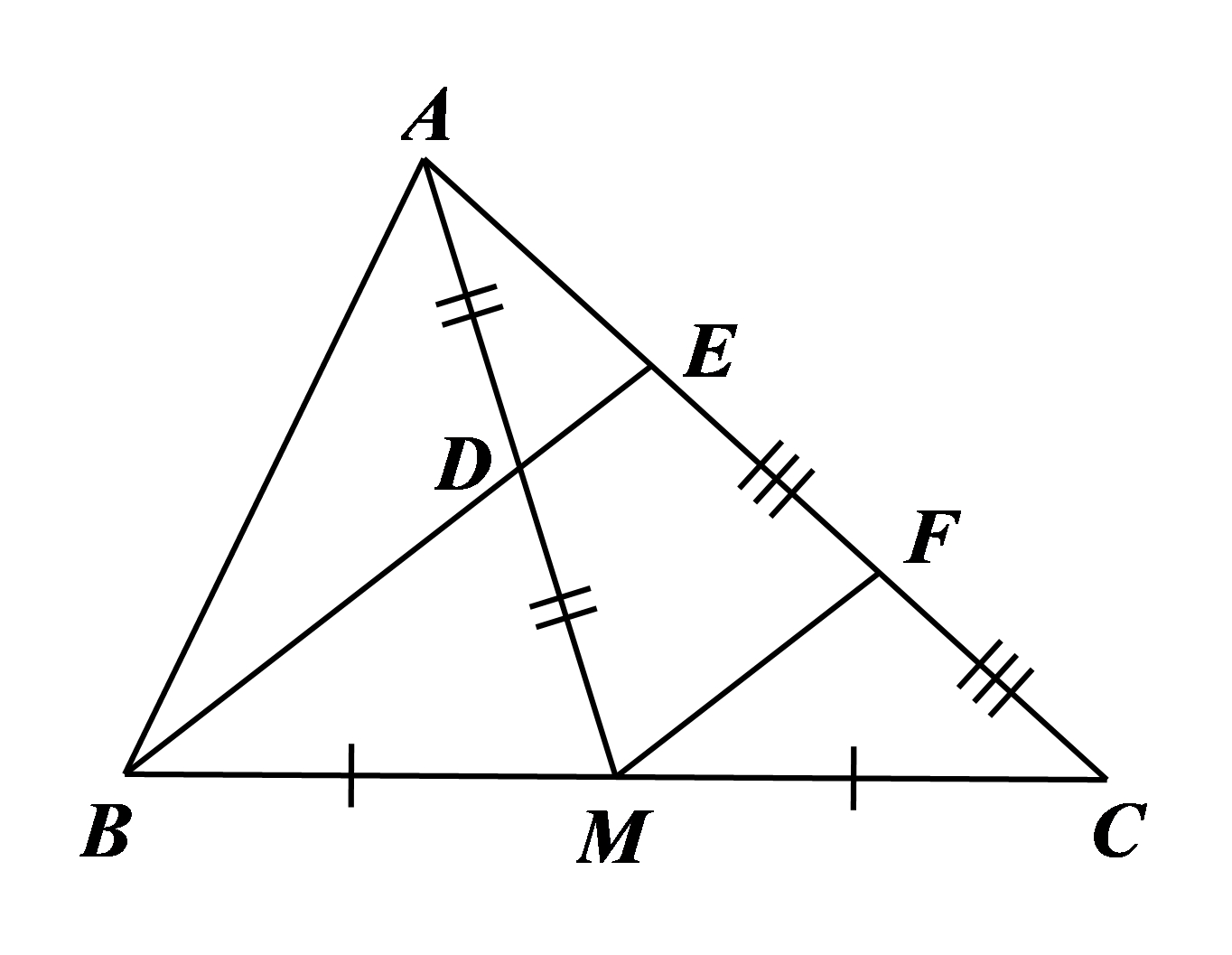
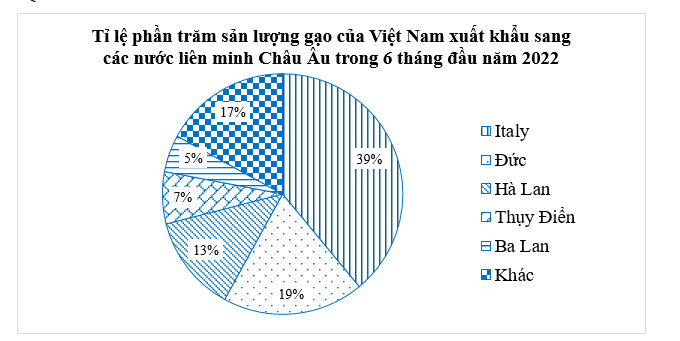
Đáp án đúng là: B
Xét \[\Delta BCE\] có \(M,\,\,F\) lần lượt là trung điểm của \(BC,\,\,EC\) nên \(MF\) là đường trung bình của tam giác, do đó \(MF\,{\rm{//}}\,BE,\) hay \(MF\,{\rm{//}}\,DE.\)
Xét \(\Delta AMF\) có \(D\) là trung điểm của \(AM\) và \(DE\,{\rm{//}}\,MF\) nên\(DE\) là đường trung bình của tam giác, do đó \(E\) là trung điểm của \(AF.\) Suy ra \(AE = EF.\)
Mà \(F\) là trung điểm của \(EC\) nên \(EF = FC,\) do đó \(AE = EF = FC\) hay \(AE = \frac{1}{3}AC = \frac{1}{3} \cdot 9 = 3{\rm{\;cm}}.\)
Câu 2
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.