Câu hỏi:

20/09/2025 184

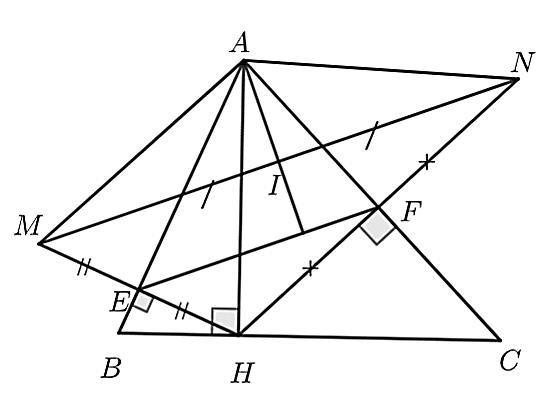
Cho tam giác $ABC$ có đường cao $AH$. Kẻ $HE \bot AB$ tại $E$ kéo dài lấy $ME = HE$. Kẻ $HF \bot AC$ tại $F$, kéo dài $HF$ lấy $FN = FH$. Gọi $I$ là trung điểm của $MN$.

a) $AB$ là trung trực của $NH.$ b) $EF\parallel MN.$

c) $\Delta AMN$ cân tại $M.$ d) $AI \bot EF.$

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án: a) Sai. b) Đúng. c) Sai. d) Đúng.

⦁ Ta có $HE \bot AB$ tại $E$ và $ME = EH$.

Do đó, $AB$ là trung trực của $MH.$

Lại có $HF \bot AC$ tại $F$ và $FN = FH$.

Như vậy, $AC$ là trung trực của $NH.$ Do đó ý a) sai.

⦁ Xét tam giác $MHN$ có $E$ là trung điểm của $MH$ và $F$ là trung điểm của $HN.$

Do đó, $EF$ là đường trung bình của tam giác $HNM$.

Suy ra $EF\parallel MN.$ Do đó ý b) đúng.

$Cho tam giác $ABC$ có đường cao $AH$. Kẻ $HE \bot AB$ tại $E$ kéo dài lấy $ME = HE$. Kẻ $HF \bot AC$ tại $F$, kéo dài $HF$ lấy $FN = FH$. Gọi $I$ là trung điểm của $MN$. a) $AB$ là trung trực của $NH.$ (ảnh 1)$

⦁ Xét $\Delta EAH$ và $\Delta EAM$ có: $AE$ chung; $ME = EH$ nên $\Delta EAH = \Delta EAM$ (hai cạnh góc vuông)

Suy ra $AM = AH$ (hai cạnh tương ứng). (1)

Tương tự, ta chứng minh $\Delta FAH = \Delta FAN$ (hai cạnh góc vuông)

Suy ra $AN = AH$ (hai cạnh tương ứng. (2)

Từ (1) và (2) suy ra $AM = AN$ nên tam giác $AMN$ cân tại $A.$ Do đó ý c) sai.

⦁ Vì $I$ là trung điểm của $MN$ mà tam giác $AMN$ cân tại $A$ nên$AI$ là đường cao của $\Delta AMN.$

Mà $EF\parallel MN$ (cmt) nên $AI \bot EF.$ Do đó ý d) đúng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang cân \[ABCD,\] đáy lớn \[BC.\] Biết $\widehat A - 2\widehat B = 30^\circ .$ Tính số đo góc tại đỉnh \[D\] của hình thang (đơn vị: độ).

Xem đáp án

Lời giải

Hướng dẫn giải

Đáp số: 130.

Theo đề bài $\widehat A - 2\widehat B = 30^\circ $ nên $\widehat A = 2\widehat B + 30^\circ $.

Vì \[ABCD\] là hình thang cân nên $\widehat A + \widehat B = 180^\circ $ nên $2\widehat B + 30^\circ + \widehat B = 180^\circ $.

Suy ra $3\widehat B = 150^\circ $ hay $\widehat B = 50^\circ $ nên $\widehat A = 130^\circ .$

Do đó $\widehat A = \widehat D = 130^\circ .$

Vậy số đo góc tại đỉnh \[D\] của hình thang là $130^\circ .$

Câu 2

Biểu đồ đoạn thẳng dưới đây biểu diễn sản lượng thủy sản của nước ta qua các năm 2010; 2014; 2016; 2018; 2020 (đơn vị: nghìn tấn).

Hỏi sản lượng thủy sản của nước ta năm 2020 chiếm bao nhiêu phần trăm tổng sản lượng thủy sản của nước ta qua các năm? (Kết quả làm tròn đến hàng phần mười)

Xem đáp án

Lời giải

Hướng dẫn giải

Đáp án: $24,6$.

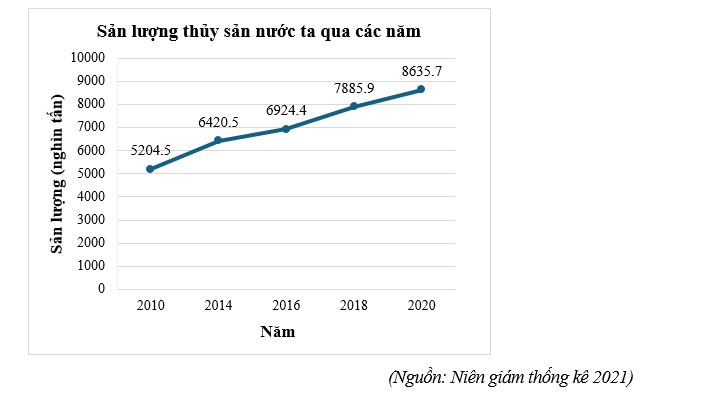
Tổng sản lượng thủy sản nước ta qua các năm là:

$5{\rm{ }}204,5 + 6{\rm{ }}420,5 + 6{\rm{ }}924,4 + 7{\rm{ }}885,9 + 8{\rm{ }}635,7 = 35{\rm{ }}071$ (nghìn tấn)

Sản lượng thủy sản của nước ta năm 2020 so với tổng sản lượng thủy sản của nước ta qua các năm chiếm số phần trăm là: $\frac{{8{\rm{ }}635,7}}{{35{\rm{ }}071}}.100\% \approx 24,6\% $.

Câu 3