Cho hai số $x\,,\,\,y$ thỏa mãn $x - y = 5$ và $xy = 3$. Tính giá trị ${x^2} + {y^2}$.

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp số: 19.

Ta có ${x^2} + {y^2} = {x^2} + 2xy + {y^2} - 2xy$

$ = {\left( {x + y} \right)^2} - 2xy$

$ = {5^2} - 2 \cdot 3 = 19$.

Vậy với $x - y = 5$ và $xy = 3$ thì giá trị của biểu thức ${x^2} + {y^2}$ bằng 19.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang cân \[ABCD,\] đáy lớn \[BC.\] Biết $\widehat A - 2\widehat B = 30^\circ .$ Tính số đo góc tại đỉnh \[D\] của hình thang (đơn vị: độ).

Xem đáp án

Lời giải

Hướng dẫn giải

Đáp số: 130.

Theo đề bài $\widehat A - 2\widehat B = 30^\circ $ nên $\widehat A = 2\widehat B + 30^\circ $.

Vì \[ABCD\] là hình thang cân nên $\widehat A + \widehat B = 180^\circ $ nên $2\widehat B + 30^\circ + \widehat B = 180^\circ $.

Suy ra $3\widehat B = 150^\circ $ hay $\widehat B = 50^\circ $ nên $\widehat A = 130^\circ .$

Do đó $\widehat A = \widehat D = 130^\circ .$

Vậy số đo góc tại đỉnh \[D\] của hình thang là $130^\circ .$

Câu 2

Biểu đồ đoạn thẳng dưới đây biểu diễn sản lượng thủy sản của nước ta qua các năm 2010; 2014; 2016; 2018; 2020 (đơn vị: nghìn tấn).

Hỏi sản lượng thủy sản của nước ta năm 2020 chiếm bao nhiêu phần trăm tổng sản lượng thủy sản của nước ta qua các năm? (Kết quả làm tròn đến hàng phần mười)

Xem đáp án

Lời giải

Hướng dẫn giải

Đáp án: $24,6$.

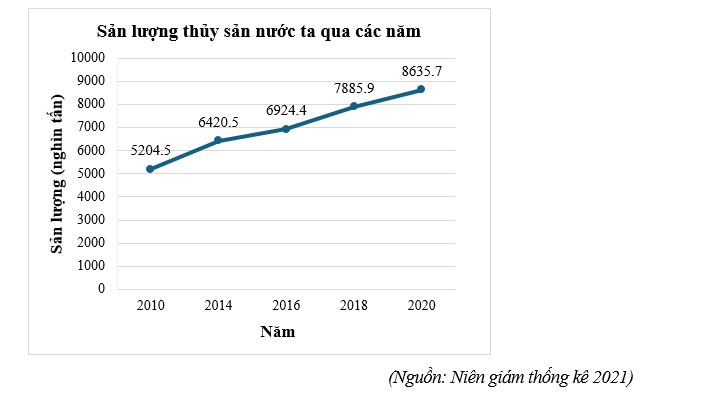
Tổng sản lượng thủy sản nước ta qua các năm là:

$5{\rm{ }}204,5 + 6{\rm{ }}420,5 + 6{\rm{ }}924,4 + 7{\rm{ }}885,9 + 8{\rm{ }}635,7 = 35{\rm{ }}071$ (nghìn tấn)

Sản lượng thủy sản của nước ta năm 2020 so với tổng sản lượng thủy sản của nước ta qua các năm chiếm số phần trăm là: $\frac{{8{\rm{ }}635,7}}{{35{\rm{ }}071}}.100\% \approx 24,6\% $.

Câu 3