Quy tắc sau đây cho ta biết CAN, CHI của năm \(X\) nào đó.
Để xác định CAN, ta tìm số dư \(r\) trong phép chia \(X\) cho 10 và tra vào Bảng 1.
Để xác định CHI, ta tìm số dư \(s\) trong phép chia \(X\) cho 12 và tra vào Bảng 2.
Bảng 1:
\(r\)
0
1
2
3
4
5
6
7
8
9
CAN
Canh
Tân
Nhâm
Quý
Giáp
Ất
Bính
Đinh
Mậu
Kỷ
Bảng 2:
\(s\)
0
1
2
3
4
5
6
7
8
9
10
11
CHI
Thân
Dâu
Tuất
Hợi
Tý
Sửu
Dần
Mão
Thìn
Tỵ
Ngọ
Mùi
a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2025.
b) Dưới sự chỉ đạo tài tình của Hưng Đạo Đại Vương Trần Quốc Tuấn, quân dân nhà Trần đã ba lần đánh thắng quân Nguyên – Mông. Chiến thắng lần thứ ba vào năm Mậu Tý (CAN là Mậu, CHI là Tý) cuối thế kỉ \(XIII\). Em hãy xác định xem năm đó là năm bao nhiêu?
Quy tắc sau đây cho ta biết CAN, CHI của năm \(X\) nào đó.
Để xác định CAN, ta tìm số dư \(r\) trong phép chia \(X\) cho 10 và tra vào Bảng 1.
Để xác định CHI, ta tìm số dư \(s\) trong phép chia \(X\) cho 12 và tra vào Bảng 2.
Bảng 1:
|
\(r\) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
CAN |
Canh |
Tân |
Nhâm |
Quý |
Giáp |
Ất |
Bính |
Đinh |
Mậu |
Kỷ |
Bảng 2:
|
\(s\) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
CHI |
Thân |
Dâu |
Tuất |
Hợi |
Tý |
Sửu |
Dần |
Mão |
Thìn |
Tỵ |
Ngọ |
Mùi |
a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2025.
b) Dưới sự chỉ đạo tài tình của Hưng Đạo Đại Vương Trần Quốc Tuấn, quân dân nhà Trần đã ba lần đánh thắng quân Nguyên – Mông. Chiến thắng lần thứ ba vào năm Mậu Tý (CAN là Mậu, CHI là Tý) cuối thế kỉ \(XIII\). Em hãy xác định xem năm đó là năm bao nhiêu?
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Ta có 2025 chia 10 được 202 dư 5 nên \(r = 5\), tra bảng 1 ta có CAN là Ất.
Có 2025 chia 12 được 168 dư 9 nên \(s = 9\), tra bảng 2 ta có CHI là Tỵ.
b) Gọi năm đó là năm \(X\). Vì sự kiện xảy ra vào thế kỉ 13 nên ta có:
\(X = \overline {12ab} ,{\rm{ }}a,b \in \mathbb{N},0 \le a,b \le 9\).
Vì năm \(X\) là năm Mậu Tý nên \(X\) chia 10 dư 8, do đó, \(X = \overline {12a8} \).
Lại có \(X\) là năm Mậu Tý nên \(X\) chia cho 12 dư 4 nên \(\left( {12 \cdot 100 + 10 \cdot a + 8} \right) - 4\) chia hết cho 12.
Suy ra \(\left( {10a + 4} \right) \vdots 12\).
Lại có \(0 \le a \le 9\) nên có \(a = 2,a = 8\).
Ta được các năm 1228 và 1288.
Vì sự kiện xảy ra vào cuối thế kì 13 nên năm đó là 1288.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \[{2^x} + {2^{x + 1}} + {2^{x + 2}} + ... + {2^{x + 2020}} = {2^{2024}} - 8\]
\[{2^x} + {2^x} \cdot 2 + {2^x} \cdot {2^2} + ... + {2^x} \cdot {2^{2020}} = {2^{2021}} \cdot {2^3} - {2^3}\]
\[{2^x} \cdot \left( {1 + 2 + {2^2} + ... + {2^{2020}}} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\].
Đặt \[A = 1 + 2 + {2^2} + ... + {2^{2020}}\]
\[2A = 2 + {2^2} + {2^3} + ... + {2^{2021}}\]
\[2A - A = 2 + {2^2} + {2^3} + ... + {2^{2021}} - \left( {1 + 2 + {2^2} + {2^3} + ... + {2^{2020}}} \right)\]
\[A = {2^{2021}} - 1\]
Do đó, \[{2^x} \cdot \left( {{2^{2021}} - 1} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\]
Suy ra \[{2^x} = {2^3}\], do đó \[x = 3\].
Lời giải
Hướng dẫn giải
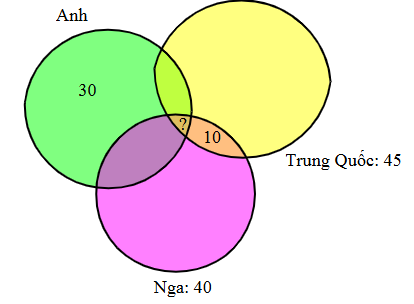
Số đại biểu nói được tiếng Nga hoặc tiếng Trung Quốc là: \(100 - 30 = 70\) (đại biểu).
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Trung Quốc là: \(70 - 45 = 25\) (đại biểu).
Số đại biểu nói được tiếng Trung Quốc nhưng không nói được tiếng Nga là: \(70 - 40 = 30\) (đại biểu).
Số đại biểu nói được tiếng Nga và tiếng Trung Quốc là: \(70 - \left( {25 + 30} \right) = 15\) (đại biểu).
Số đại biểu nói được cả ba thứ tiếng là: \(15 - 10 = 5\) (đại biểu).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.