Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu có thể sử dụng ít nhất một trong ba thứ tiếng: Nga, Trung Quốc và Anh. Biết rằng có 30 đại biểu chỉ nói được tiếng Anh, 40 đại biểu nói được tiếng Nga, 45 đại biểu nói được tiếng trung và 10 đại biểu chỉ nói được hai thứ tiếng Nga và
Trung Quốc. Hỏi có bao nhiêu đại biểu nói được cả ba thứ tiếng?
Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu có thể sử dụng ít nhất một trong ba thứ tiếng: Nga, Trung Quốc và Anh. Biết rằng có 30 đại biểu chỉ nói được tiếng Anh, 40 đại biểu nói được tiếng Nga, 45 đại biểu nói được tiếng trung và 10 đại biểu chỉ nói được hai thứ tiếng Nga và
Trung Quốc. Hỏi có bao nhiêu đại biểu nói được cả ba thứ tiếng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
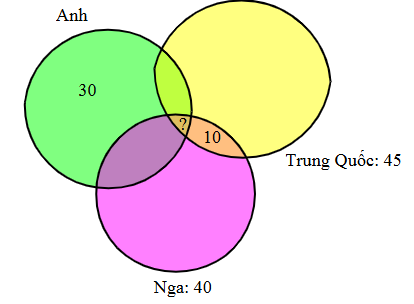
Số đại biểu nói được tiếng Nga hoặc tiếng Trung Quốc là: \(100 - 30 = 70\) (đại biểu).
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Trung Quốc là: \(70 - 45 = 25\) (đại biểu).
Số đại biểu nói được tiếng Trung Quốc nhưng không nói được tiếng Nga là: \(70 - 40 = 30\) (đại biểu).
Số đại biểu nói được tiếng Nga và tiếng Trung Quốc là: \(70 - \left( {25 + 30} \right) = 15\) (đại biểu).
Số đại biểu nói được cả ba thứ tiếng là: \(15 - 10 = 5\) (đại biểu).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \[{2^x} + {2^{x + 1}} + {2^{x + 2}} + ... + {2^{x + 2020}} = {2^{2024}} - 8\]
\[{2^x} + {2^x} \cdot 2 + {2^x} \cdot {2^2} + ... + {2^x} \cdot {2^{2020}} = {2^{2021}} \cdot {2^3} - {2^3}\]
\[{2^x} \cdot \left( {1 + 2 + {2^2} + ... + {2^{2020}}} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\].
Đặt \[A = 1 + 2 + {2^2} + ... + {2^{2020}}\]
\[2A = 2 + {2^2} + {2^3} + ... + {2^{2021}}\]
\[2A - A = 2 + {2^2} + {2^3} + ... + {2^{2021}} - \left( {1 + 2 + {2^2} + {2^3} + ... + {2^{2020}}} \right)\]
\[A = {2^{2021}} - 1\]
Do đó, \[{2^x} \cdot \left( {{2^{2021}} - 1} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\]
Suy ra \[{2^x} = {2^3}\], do đó \[x = 3\].
Lời giải
Hướng dẫn giải
Theo đề, ô thứ nhất bỏ vào 1 hạt.
Ô thứ hai bỏ vào \(2 = {2^1}\) (hạt).
Ô thứ ba bỏ vào \(4 = {2^2}\) (hạt).
Ô thứ tư vỏ vào \(8 = {2^3}\) (hạt) và cứ như vậy, ở ô tiếp theo số hạt gạo gấp đôi ô trước đó nên ô thứ 64 bỏ vào \({2^{63}}\) hạt.
Khi đó, tổng số hạt gạo được Minh xếp lên bàn cờ vua là:
\(S = 1 + {2^1} + {2^2} + {2^3} + ... + {2^{63}}\)
\(2S = {2^1} + {2^2} + {2^3} + ... + {2^{64}}\)
Suy ra \(2S - S = {2^{64}} - 1\) hay \(S = {2^{64}} - 1\).
Vậy tổng số hạt gạo được Minh xếp lên trên bàn cờ vua là \({2^{64}} - 1\) hạt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo