Trên một bàn cờ vua, Minh muốn xếp gạo vào ô vuông theo quy luật sau: ô thứ nhất bỏ vào 1 hạt, ô thứ hai bỏ vào 2 hạt, ô thứ ba bỏ vào 4 hạt, ô thứ tư bỏ vào 8 hạt, ở ô tiếp theo xếp số hạt gạo gấp đôi ô trước đó đến khi hết 64 ô trong bàn cờ. Hãy tính tổng số hạt gạo được Minh xếp trên bản cờ vua.
Trên một bàn cờ vua, Minh muốn xếp gạo vào ô vuông theo quy luật sau: ô thứ nhất bỏ vào 1 hạt, ô thứ hai bỏ vào 2 hạt, ô thứ ba bỏ vào 4 hạt, ô thứ tư bỏ vào 8 hạt, ở ô tiếp theo xếp số hạt gạo gấp đôi ô trước đó đến khi hết 64 ô trong bàn cờ. Hãy tính tổng số hạt gạo được Minh xếp trên bản cờ vua.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Theo đề, ô thứ nhất bỏ vào 1 hạt.
Ô thứ hai bỏ vào \(2 = {2^1}\) (hạt).
Ô thứ ba bỏ vào \(4 = {2^2}\) (hạt).
Ô thứ tư vỏ vào \(8 = {2^3}\) (hạt) và cứ như vậy, ở ô tiếp theo số hạt gạo gấp đôi ô trước đó nên ô thứ 64 bỏ vào \({2^{63}}\) hạt.
Khi đó, tổng số hạt gạo được Minh xếp lên bàn cờ vua là:
\(S = 1 + {2^1} + {2^2} + {2^3} + ... + {2^{63}}\)
\(2S = {2^1} + {2^2} + {2^3} + ... + {2^{64}}\)
Suy ra \(2S - S = {2^{64}} - 1\) hay \(S = {2^{64}} - 1\).
Vậy tổng số hạt gạo được Minh xếp lên trên bàn cờ vua là \({2^{64}} - 1\) hạt.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \[{2^x} + {2^{x + 1}} + {2^{x + 2}} + ... + {2^{x + 2020}} = {2^{2024}} - 8\]
\[{2^x} + {2^x} \cdot 2 + {2^x} \cdot {2^2} + ... + {2^x} \cdot {2^{2020}} = {2^{2021}} \cdot {2^3} - {2^3}\]
\[{2^x} \cdot \left( {1 + 2 + {2^2} + ... + {2^{2020}}} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\].
Đặt \[A = 1 + 2 + {2^2} + ... + {2^{2020}}\]
\[2A = 2 + {2^2} + {2^3} + ... + {2^{2021}}\]
\[2A - A = 2 + {2^2} + {2^3} + ... + {2^{2021}} - \left( {1 + 2 + {2^2} + {2^3} + ... + {2^{2020}}} \right)\]
\[A = {2^{2021}} - 1\]
Do đó, \[{2^x} \cdot \left( {{2^{2021}} - 1} \right) = {2^3} \cdot \left( {{2^{2021}} - 1} \right)\]
Suy ra \[{2^x} = {2^3}\], do đó \[x = 3\].
Lời giải
Hướng dẫn giải
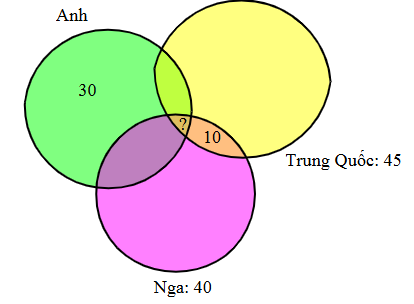
Số đại biểu nói được tiếng Nga hoặc tiếng Trung Quốc là: \(100 - 30 = 70\) (đại biểu).
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Trung Quốc là: \(70 - 45 = 25\) (đại biểu).
Số đại biểu nói được tiếng Trung Quốc nhưng không nói được tiếng Nga là: \(70 - 40 = 30\) (đại biểu).
Số đại biểu nói được tiếng Nga và tiếng Trung Quốc là: \(70 - \left( {25 + 30} \right) = 15\) (đại biểu).
Số đại biểu nói được cả ba thứ tiếng là: \(15 - 10 = 5\) (đại biểu).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo