Một công ty muốn xây dựng một đường ống dẫn dầu từ điểm \[A\] trên bờ biển đến một điểm \[C\] trên một hòn đảo như hình vẽ. Giá để xây dựng đường ống trên bờ là \[40\,\,000{\rm{ USD}}\] mỗi km và \[130\,\,000{\rm{ USD}}\] mỗi km để xây dưới nước. Hỏi công ty nên xây đường ống theo phương án nào để tiết kiệm chi phí nhất? Biết rằng công ty đưa ra ba phương án:
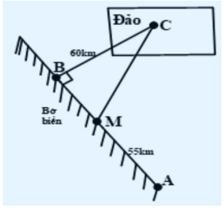
Phương án 1: Xây đường ống từ điểm \[A\] trên bờ đến điểm \[C\] trên đảo.
Phương án 2: Xây đường ống từ điểm \[A\] đến điểm \(M\) trên bờ biển, rồi xây đường ống từ điểm \(M\) đến điểm \[C\] trên hòn đảo.
Phương án 3: Xây đường ống từ điểm \[A\] đến điểm \(B\) trên bờ biển, rồi xây đường ống từ điểm \(B\) đến điểm \[C\] trên hòn đảo. Biết \(BC = 60\,\;{\rm{km}},\,\,AB = 100\,\;{\rm{km}},\,\,AM = 55\;\,{\rm{km}}{\rm{.}}\)
Một công ty muốn xây dựng một đường ống dẫn dầu từ điểm \[A\] trên bờ biển đến một điểm \[C\] trên một hòn đảo như hình vẽ. Giá để xây dựng đường ống trên bờ là \[40\,\,000{\rm{ USD}}\] mỗi km và \[130\,\,000{\rm{ USD}}\] mỗi km để xây dưới nước. Hỏi công ty nên xây đường ống theo phương án nào để tiết kiệm chi phí nhất? Biết rằng công ty đưa ra ba phương án:

Quảng cáo
Trả lời:
Hướng dẫn giải
b) Độ dài đoạn \(BM\) là: \(BM = AB - AM = 100 - 5 = 45\;\;({\rm{km)}}\).
Xét \(\Delta MBC\) vuông tại \(B\), áp dụng định lý Pythagore ta có:
\(CM = \sqrt {B{C^2} + B{M^2}} = \sqrt {{{60}^2} + {{45}^2}} = \sqrt {5\,\,625} = 75\) km.
Xét tam giác \(ABC\) vuông tại \(B\), áp dụng định lý Pythagore ta có:
\(AC = \sqrt {B{C^2} + A{B^2}} = \sqrt {{{60}^2} + {{100}^2}} = \sqrt {13\,\,600} \approx 116,62\;{\rm{km}}\).
Tổng số tiền xây dựng theo phương án 1:
\({T_1} = 130\,\,000 \cdot 116,62 = 15\,\,160\,\,474,93\) (USD)
Tổng số tiền xây dựng theo phương án 2:
\({T_2} = 40\,\,000 \cdot 55 + 130\,\,000 \cdot 75 = 11\,\,950\,\,000\) (USD)
Tổng số tiền xây dựng theo phương án 3:
\({T_3} = 40\,\,000 \cdot 100 + 130\,\,000 \cdot 60 = 11\,\,800\,\,000\) (USD)
Do \({T_1} > {T_2} > {T_3}\) nên phương án 3 là phương án xây dựng đường ống mà tiết kiệm chi phí nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\)
\(2{x^2} + 2{y^2} - 6x - 6y + 2xy + 6 = 0\)
\({\left( {x + y - 2} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\).
Từ đó suy ra \[x = y = 1.\]
Thay \(x = y = 1\) vào biểu thức Q ta được \(Q = {\left( {1 - 1} \right)^{2023}} + {\left( {1 - 2} \right)^{2024}} + {1^{2025}} = 0 + 1 + 1 = 2\).
Vậy \[Q = 2.\]
Lời giải
Hướng dẫn giải
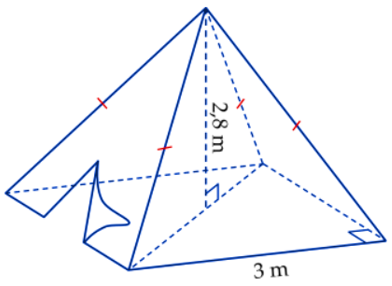
a) Thể tích kim tự tháp là: \[V = \frac{1}{3}.\,{34^2}.\,21 = 8\,\,092\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Diện tích một viên gạch hình vuông là: \[S = {\left( {0,6} \right)^2} = 0,36\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Số viên gạch hình vuông cần dùng là: \(\frac{{1\,\,000}}{{0,36}} \approx 2\,\,778\) (viên)
c) Số tấm kính hình thoi trên mỗi mặt là: \(\frac{{17\,.\,\left( {17 + 1} \right)}}{2} = 153\) (tấm)
Vậy có 153 tấm kính hình thoi trên mỗi mặt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.