Tìm giá trị nhỏ nhất của biểu thức:
e) $\left| {x - 1} \right| + \left| {x - 2} \right|$;

Câu hỏi trong đề: Đề cương ôn tập giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

e) Ta có $\left| {x - 1} \right| + \left| {x - 2} \right| = \left| {x - 1} \right| + \left| {2 - x} \right| \ge \left| {\left( {x - 1} \right) + \left( {2 - x} \right)} \right| = 1$.

Dấu xảy ra khi và chỉ khi $\left( {x - 1} \right)\left( {2 - x} \right) \ge 0$ nên \[\left\{ \begin{array}{l}x - 1 \ge 0\\2 - x \ge 0\end{array} \right.\] hoặc $\left\{ \begin{array}{l}x - 1 \le 0\\2 - x \le 0\end{array} \right.$.

Khi đó \[\left\{ \begin{array}{l}x \ge 1\\x \le 2\end{array} \right.\] hoặc $\left\{ \begin{array}{l}x \le 1\\x \ge 2\end{array} \right.$. Do đó $1 \le x \le 2$.

Vậy giá trị nhỏ nhất của biểu thức đã cho là 1 khi $1 \le x \le 2$.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vẽ bên.

a) Kể tên các cặp góc đối đỉnh trong hình.
b) Vẽ $Om$ là tia phân giác của góc $\widehat {xOz}$. Tính số đo góc \[\widehat {tOy};\,\,\widehat {xOt};\]$\widehat {mOx}$.

Xem đáp án

Lời giải

Kể tên các cặp góc đối đỉnh trong hình. (ảnh 2)

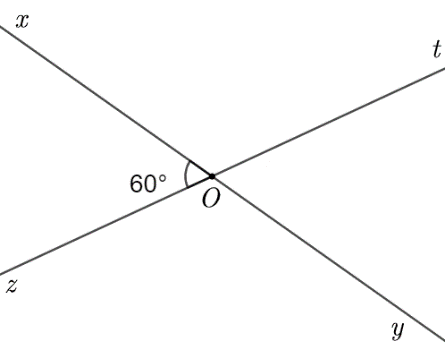
a) Các cặp góc đối đỉnh trong hình là: $\widehat {xOz}$ và $\widehat {tOy}$; $\widehat {xOt}$ và $\widehat {tOy}$.

b) Từ hình vẽ ta thấy $\widehat {xOz} = 60^\circ $

Vì $\widehat {xOz}$ và $\widehat {tOy}$ là hai góc đối đỉnh nên $\widehat {xOz} = \widehat {tOy} = 60^\circ $.

Vì góc $\widehat {xOz}$và $\widehat {xOt}$ là hai góc kề bù nên $\widehat {xOz} + \widehat {xOt} = 180^\circ $.

Suy ra $\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 60^\circ = 120^\circ $.

Do đó $\widehat {xOt} = 120^\circ $.

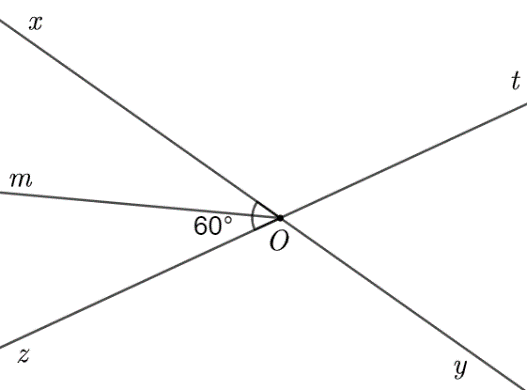
Vì $Om$ là tia phân giác của $\widehat {xOz}$ nên $\widehat {mOx} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ $.

Vậy $\widehat {tOy} = 60^\circ ;\,\,\widehat {xOt} = 120^\circ ;\,\,\widehat {mOx} = 30^\circ $.

Câu 2

Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{14 - x}}{{4 - x}}\] với mọi $x \in \mathbb{Z}$. Khi đó \[x\] nhận giá trị nguyên nào?

Xem đáp án

Lời giải

Hướng dẫn giải

Ta có \[P = \frac{{14 - x}}{{4 - x}} = 1 + \frac{{10}}{{4 - x}}\].

Để ${P_{\min }}$ thì ${\left( {\frac{{10}}{{4 - x}}} \right)_{{\rm{min}}}}$, mà $4 - x < 0$ và \[x\] nguyên nên $4 - x = - 1$ nên $x = 5$.

Vậy ${P_{\min }} = - 9$ khi $x = 5$.

Câu 3