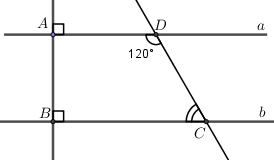
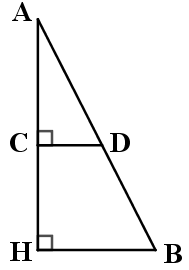
Cho hình vẽ bên biết thanh gỗ \(AB\)dựa vào tường làm thành góc \(63^\circ \) so với mặt đất, người ta dùng tiếp thanh gỗ \(CD\) đặt vuông góc với tường sao cho điểm \(D\) nằm trên thanh gỗ \(AB\). Hãytính góc tạo bởi thanh gỗ \(CD\) và thanh gỗ \(AB\).

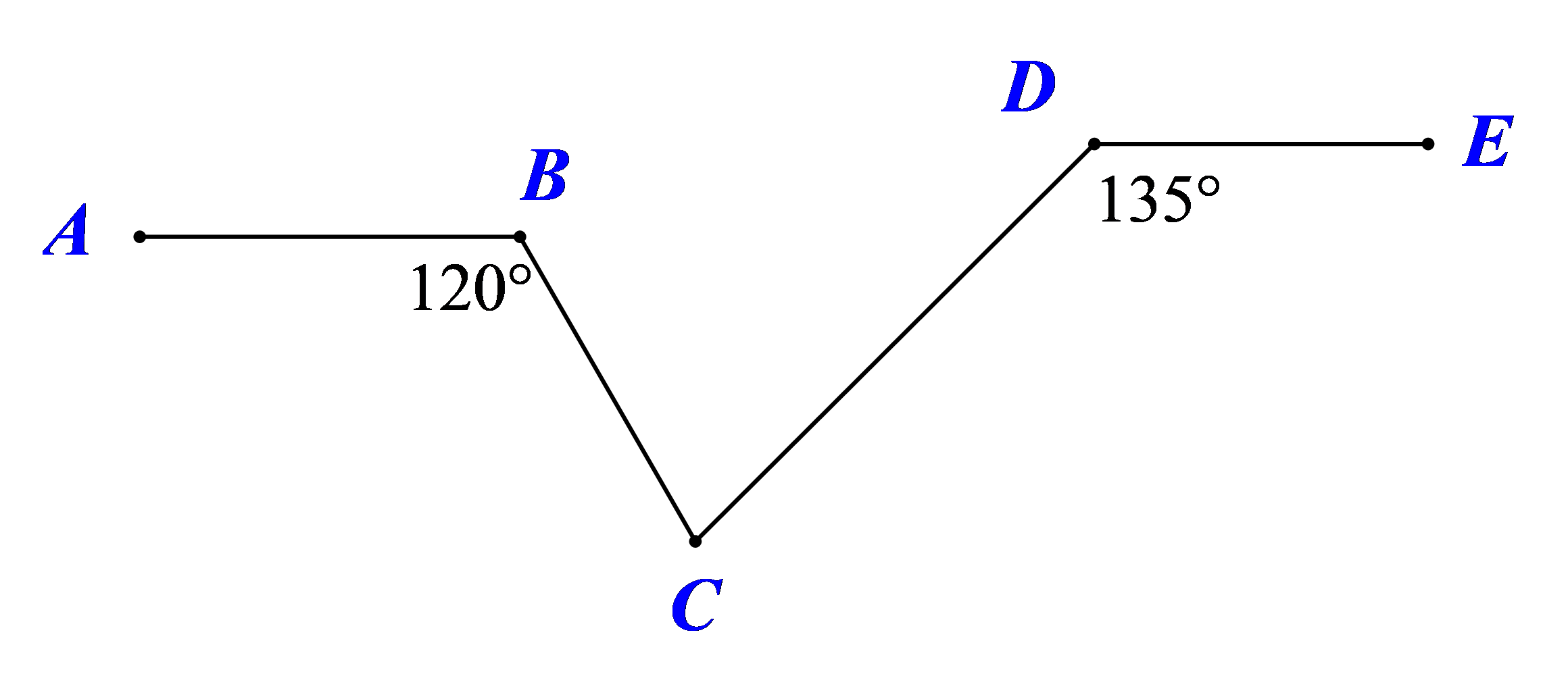
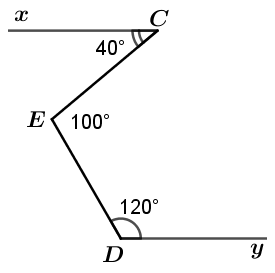
Kẻ đường thẳng qua \(C\) và song song với \[AB\].

Mà \(AB\,{\rm{//}}\,DE\) nên đường thẳng đó cũng song song với \[DE\].

Do đó \({\widehat C_1} + \widehat {ABC} = 180^\circ \) và \(\widehat {{C_2}} + \widehat {CDE} = 180^\circ \) (hai góc trong cùng phía)

Do đó, \[{\widehat C_1} = 60^\circ \] và \[\,{\widehat C_2} = 45^\circ \].

Suy ra \[\widehat {BCD} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \].

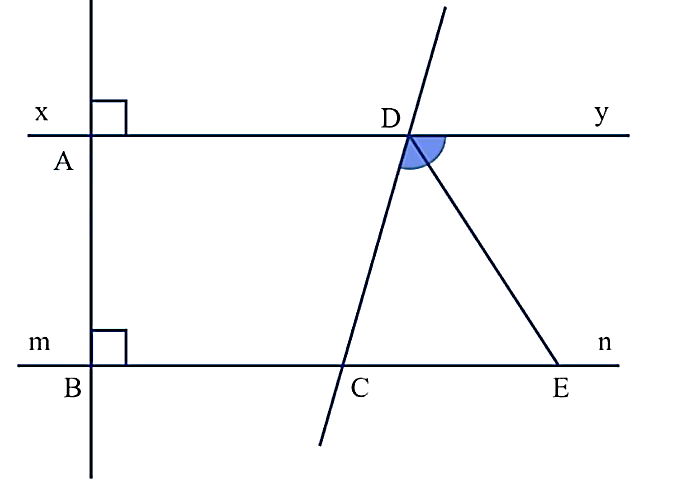
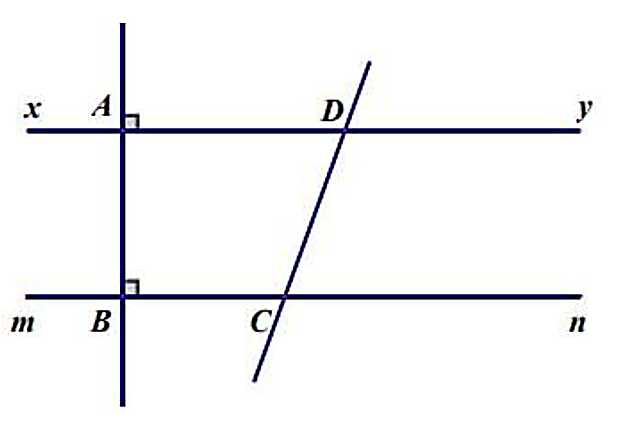
a) Ta có: \(xy \bot AB\) và \(mn \bot AB\) nên \(xy\parallel mn.\)

b) Ta có: \(\widehat {DCB} + \widehat {DCn} = 180^\circ \) (hai góc kề bù).

Suy ra \(\widehat {DCB} = 180^\circ - \widehat {DCn} = 180^\circ - 70^\circ = 110^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {DCB} = \widehat {CDy} = 110^\circ \) (hai góc so le trong).

c) Vì \(DE\) là tia phân giác của \(\widehat {CDy}\) nên \(\widehat {CDE} = \widehat {EDy} = \frac{{\widehat {CDy}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {ECD} = \widehat {ADC} = 70^\circ \) (hai góc so le trong)

Mà \(\widehat {ADE} = \widehat {ADC} + \widehat {CDE} = 70^\circ + 55^\circ = 125^\circ \).