Câu hỏi:

23/09/2025 249

Cho $\Delta ABC$ có $AB < BC$. Trên tia $BA$ lấy điểm $D$ sao cho $BD = BC$. Trên tia phân giác của $\widehat B$ cắt$AC$ ở $E$. Gọi $K$ là trung điểm của $DC$.

a) Chứng minh $\Delta BED = \Delta BEC$.

b) Chứng minh $EK \bot DC$.

c) Chứng minh $B,\,\,K,\,\,E$ thẳng hàng.

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

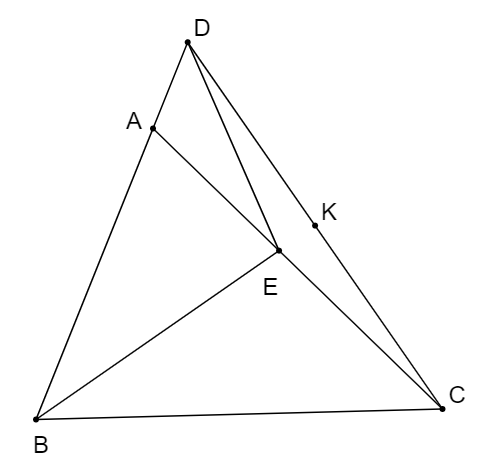
$Chứng minh $\Delta BED = \Delta BEC$. (ảnh 1)$

a) Xét $\Delta BED$ và $\Delta BEC$ ta có

$BD = BC$ (giả thiết)

$\widehat {DBE} = \widehat {CBE}$ ($BE$ là phân giác của $\widehat {DBC}$)

$BE$ chung

Do đó $\Delta BED = \Delta BEC$ (c.g.c)

Suy ra $ED = EC$ (hai cạnh tương ứng)

b) Xét \[\Delta DEK\] và \[\Delta CEK\] có

$ED = EC$ (chứng minh trên)

\[DK = CK\] ($K$ là trung điểm của $CD$)

\[EK\] chung

Do đó \[\Delta DEK = \Delta CEK\,\,\](c.c.c)

Suy ra \[\widehat {DKE} = \widehat {CKE}\] (hai góc tương ứng)

Ta có \[\widehat {DKE} + \widehat {CKE} = 180^\circ \] (hai góc kề bù) nên \[\widehat {DKE} = \widehat {CKE} = \frac{{180^\circ }}{2} = 90^\circ \].

Suy ra \[EK \bot CD\] \[\,\,\,\left( 1 \right)\]

c) Xét \[\Delta DBK\] và \[\Delta CBK\] có

$BD = BC$ (giả thiết)

\[DK = CK\] ($K$ là trung điểm của $CD$)

\[BK\] chung

Do đó \[\Delta DBK = \Delta CBK\,\,\](c.c.c)

Suy ra \[\widehat {DKB} = \widehat {CKB}\] (hai góc tương ứng)

Ta có \[\widehat {DKB} + \widehat {CKB} = 180^\circ \] (kề bù) nên \[\widehat {DKB} = \widehat {CKB} = \frac{{180^\circ }}{2} = 90^\circ \].

Suy ra \[BK \bot CD\,\,\,\left( 2 \right)\]

Từ \[\,\left( 1 \right)\] và \[\,\left( 2 \right)\] suy ra $B,K,E$ thẳng hàng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm \[x\]

c) \[\frac{{x - 214}}{{86}} + \frac{{x - 132}}{{84}} + \frac{{x - 54}}{{82}} = 6\];

Xem đáp án

Lời giải

c) \[\frac{{x - 214}}{{86}} + \frac{{x - 132}}{{84}} + \frac{{x - 54}}{{82}} = 6\]

\[x\left( {\frac{1}{{86}} + \frac{1}{{84}} + \frac{1}{{82}}} \right) = 6 + \frac{{214}}{{86}} + \frac{{132}}{{84}} + \frac{{54}}{{82}}\]

\[x\left( {\frac{1}{{86}} + \frac{1}{{84}} + \frac{1}{{82}}} \right) = \left( {1 + \frac{{214}}{{86}}} \right) + \left( {2 + \frac{{132}}{{84}}} \right) + \left( {3 + \frac{{54}}{{82}}} \right)\]

\[x\left( {\frac{1}{{86}} + \frac{1}{{84}} + \frac{1}{{82}}} \right) = \frac{{300}}{{86}} + \frac{{300}}{{84}} + \frac{{300}}{{82}}\]

\[x\left( {\frac{1}{{86}} + \frac{1}{{84}} + \frac{1}{{82}}} \right) = 300\left( {\frac{1}{{86}} + \frac{1}{{84}} + \frac{1}{{82}}} \right)\]

\[x = 300\]

Vậy \[x = 300\].

Câu 2

Tìm \[x\]:

a) \[\frac{{x + 1}}{{99}} + \frac{{x + 2}}{{98}} + \frac{{x + 3}}{{97}} + \frac{{x + 4}}{{96}} = - 4\];

Xem đáp án

Lời giải

a) \[\frac{{x + 1}}{{99}} + \frac{{x + 2}}{{98}} + \frac{{x + 3}}{{97}} + \frac{{x + 4}}{{96}} = - 4\]

\[x\left( {\frac{1}{{99}} + \frac{1}{{98}} + \frac{1}{{97}} + \frac{1}{{96}}} \right) + \left( {\frac{1}{{99}} + \frac{2}{{98}} + \frac{3}{{97}} + \frac{4}{{96}}} \right) = - 4\]

\[x\left( {\frac{1}{{99}} + \frac{1}{{98}} + \frac{1}{{97}} + \frac{1}{{96}}} \right) = - \left( {1 + \frac{1}{{99}}} \right) - \left( {1 + \frac{2}{{98}}} \right) - \left( {1 + \frac{3}{{97}}} \right) - \left( {1 + \frac{4}{{96}}} \right)\]

\[x\left( {\frac{1}{{99}} + \frac{1}{{98}} + \frac{1}{{97}} + \frac{1}{{96}}} \right) = - \frac{{100}}{{99}} - \frac{{100}}{{98}} - \frac{{100}}{{97}} - \frac{{100}}{{96}}\]

\[x\left( {\frac{1}{{99}} + \frac{1}{{98}} + \frac{1}{{97}} + \frac{1}{{96}}} \right) = - 100.\left( {\frac{1}{{99}} + \frac{1}{{98}} + \frac{1}{{97}} + \frac{1}{{96}}} \right)\]

\[x = - 100\].

Vậy \[x = - 100\].

Câu 3