Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác \(ABC\) có \(AB = 7\), \(AC = 8\) và \(\widehat A = 60^\circ \). Độ dài của cạnh \(BC\) bằng
Quảng cáo
Trả lời:
Áp dụng định lí côsin trong tam giác ABC, có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat A\)\( = 49 + 64 - 2.7.8.\cos 60^\circ = 57\)\( \Rightarrow BC = \sqrt {57} \). Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
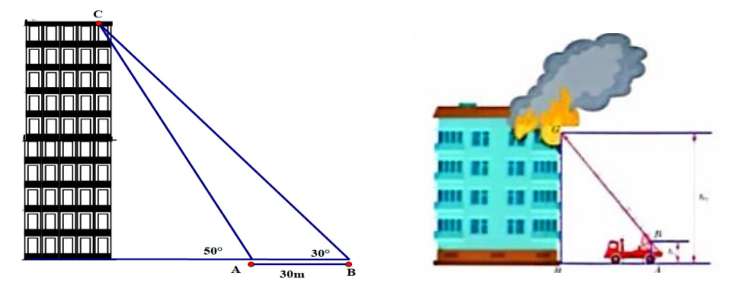
a) Xét tam giác ABC có \(\widehat {BAC} = 180^\circ - 50^\circ = 130^\circ ,\widehat {ABC} = 30^\circ \) nên \(\widehat {ACB} = 180^\circ - 130^\circ - 30^\circ = 20^\circ \).
b) Áp dụng định lí sin cho tam giác ABC ta được
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\) \( \Rightarrow \frac{{30}}{{\sin 20^\circ }} = \frac{{AC}}{{\sin 30^\circ }}\) \( \Rightarrow AC = \frac{{30.\sin 30^\circ }}{{\sin 20^\circ }} \approx 43,9\) m.
c) Xét tam giác vuông CHA vuông tại H nên \(CH = AC.\sin 50^\circ \approx 33,6\) m.
d) Chân thang cách mặt đất 1,8 m ta có CK = CH – HK = 33,6 – 1,8 = 31,8 m.
Khi đó khoảng cách tới chân tòa nhà xa nhất có thể là:
\(KD = \sqrt {C{D^2} - C{K^2}} = \sqrt {{{40}^2} - 31,{8^2}} \approx 24,3\) m.
Đáp án: a) Sai; b) Đúng; c) Sai; d) Sai.
Lời giải
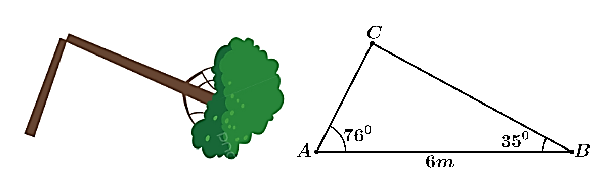
Ta có \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {76^\circ + 35^\circ } \right) = 69^\circ \).
Theo định lí sin \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)\( \Rightarrow AC = \frac{{AB.\sin B}}{{\sin C}} = \frac{{6.\sin 35^\circ }}{{\sin 69^\circ }}\).
Có \(BC = \frac{{AB.\sin A}}{{\sin C}} = \frac{{6.\sin 76^\circ }}{{\sin 69^\circ }}\).
Suy ra \(AC + BC = \frac{{6.\sin 35^\circ }}{{\sin 69^\circ }} + \frac{{6.\sin 76^\circ }}{{\sin 69^\circ }} \approx 9,92\).
Vậy chiều cao ban đầu của cây xấp xỉ bằng 9,92 m.
Trả lời: 9,92.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.