Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:
\[\begin{array}{l}653 & 632 & 609 & 572 & 565 & 535 & 516 & 514 & 508 & 505 & \\504 & 504 & 503 & 499 & 496 & 492{\rm{ }}.\end{array}\]
(Theo: https://www.premierleague.com/)
Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.
Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:
\[\begin{array}{l}653 & 632 & 609 & 572 & 565 & 535 & 516 & 514 & 508 & 505 & \\504 & 504 & 503 & 499 & 496 & 492{\rm{ }}.\end{array}\]
(Theo: https://www.premierleague.com/)
Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.
Câu hỏi trong đề: Đề kiểm tra Mẫu số liệu ghép nhóm (có lời giải) !!
Quảng cáo
Trả lời:
Giá trị nhỏ nhất của mẫu số liệu là 492, giá trị lớn nhất của mẫu số liệu là 653, do đó khoảng biến thiên của mẫu số liệu là \[\;R = 653 - 492 = 161\]. Ta cần chia thành bảy nhóm có độ dài bằng nhau. Để cho thuận tiện, ta chọn đầu mút trái của nhóm đầu tiên là 485 và đầu mút phải của nhóm cuối cùng bằng 660 và độ dài của mỗi nhóm bằng 25 ta được các nhóm là \[\left[ {485;510} \right),\left[ {510;535} \right),\left[ {535;560} \right),\left[ {560;585} \right),\left[ {585;610} \right),\left[ {610;635} \right),\left[ {635;660} \right].\]Đếm số giá trị thuộc mỗi nhóm, ta có mẫu số liệu ghép nhóm như sau:
|
Thời gian |
\([485;510)\) |
\([510;535)\) |
\([535;560)\) |
\([560;585)\) |
\([585;610)\) |
\([610;635)\) |
\([635;660]\) |
|
Số cầu thủ |
8 |
2 |
1 |
2 |
1 |
1 |
1 |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
Giá trị lớn nhất và nhỏ nhất lần lượt là \({x_{\max }} = 145,{x_{\min }} = 129\).
Khoảng biến thiên: \(R = {x_{\max }} - {x_{\min }} = 16\). Tổng độ dài sáu nhóm: \(6.3 = 18\).
Chọn đầu mút trái nhóm đầu tiên là 127,5, đầu mút phải nhóm cuối là 145,5 .
Ta có mẫu số liệu ghép nhóm sau:
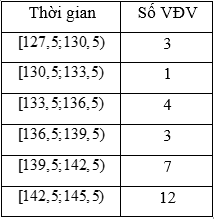
Lời giải
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
Bảng thống kê số lượng cam theo giá trị đại diện:
|
Cân nặng đại diện (gam) |
152,5 |
157,5 |
162,5 |
167,5 |
172,5 |
|
Số quả cam ở lô hàng \(A\) |
2 |
6 |
12 |
4 |
1 |
|
Số quả cam ở lô hàng \(B\) |
1 |
3 |
7 |
10 |
4 |
Cân nặng trung bình của mỗi quả cam ở lô \(A\) là:
\({\bar x_A} = \frac{{152,5 \cdot 2 + 157,5 \cdot 6 + 162,5 \cdot 12 + 167,5 \cdot 4 + 172,5 \cdot 1}}{{25}} = 161,7{\rm{ (gam)}}{\rm{. }}\)
Cân nặng trung bình của mỗi quả cam ở lô \(B\) là:
\({\bar x_B} = \frac{{152,5 \cdot 1 + 157,5 \cdot 3 + 162,5 \cdot 7 + 167,5 \cdot 10 + 172,5 \cdot 4}}{{25}} = 165,1{\rm{ (gam)}}{\rm{. }}\)
Ta thấy \({\bar x_A} < {\bar x_B}\). Vậy nếu so sánh theo số trung bình thì cam ở lô hàng \(B\) nặng hơn cam ở lô hàng \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Câu 7: Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau: Giá trị đại diện của nhóm \[\left[ {30;40} \right)\] là: A. \(40\). B. \(30\). C. \(35\). D. \(9\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/9-1759630031.png)