Cho số \(n = \overline {a2b.} \) Biết rằng \(b\) là số nguyên tố nhỏ nhất và \(a\) hợp số nhỏ nhất.
a) \(b = 3.\)
b) \(a = 4.\)
c) Số \(n\) là số nguyên tố.
d) Phân tích \(n - 2\) ra thừa số nguyên tố ta được \(n - 2 = {2^2} \cdot 3 \cdot 5 \cdot 7.\)
Quảng cáo
Trả lời:
a) Sai.
Vì \(b\) là số nguyên tố nhỏ nhất nên \(b = 2.\)
b) Đúng.
Vì \(a\) là hợp số nhỏ nhất nên \(a = 4.\)
c) Sai.
Ta có: \(n = 422 = \left( {2 \cdot 211} \right) \vdots 2\) nên \(2\) là ước của 422. Do đó, \(n\) có nhiều hơn hai ước nên \(n\) là hợp số.
d) Đúng.
Ta có: \(n - 2 = 422 - 2 = 420.\) Phân tích 420 ra thừa số nguyên tố ta được: \(420 = {2^2} \cdot 3 \cdot 5 \cdot 7.\)
Vậy \(n - 2\) phân tích ra thừa số nguyên tố ta được \(n - 2 = {2^2} \cdot 3 \cdot 5 \cdot 7.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
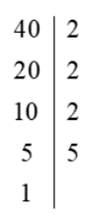
Nhận thấy, số được phân tích là \(a = 40\).
b) Sai.
Ta có: \(a = 40 = {2^3} \cdot 5\).
c) Đúng.
Vì \(a = 40 = {2^3} \cdot 5\) nên các ước nguyên tố của \(a\) là 2 và 5.
d) Đúng.
Tất cả các ước của \(a\) là \(\left\{ {1;\,\,2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,20;\,\,40} \right\}\).
Lời giải
Chọn đáp án B
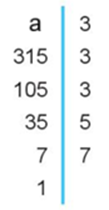
Ta có: \(140 = {2^2} \cdot 5 \cdot 7\).
Mà \({a^2} \cdot b \cdot 7 = 140\) nên \({a^2} \cdot b \cdot 7 = {2^2} \cdot 5 \cdot 7\).
Do đó, \(a = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.