Lớp 10A có 45 học sinh trong đó có 20 học sinh nam và 25 học sinh nữ. Trong bài kiểm tra môn Toán cả lớp có 22 học sinh đạt điểm giỏi (trong đó có 10 học sinh nam và 12 học sinh nữ). Giáo viên chọn ngẫu nhiên một học sinh từ danh sách lớp. Tính xác suất để giáo viên chọn được một học sinh đạt điểm giỏi môn Toán biết học sinh đó là học sinh nam.
A. \(\frac{1}{2}\).
B. \(\frac{4}{5}\).
C. \(\frac{3}{5}\).
D. \(\frac{4}{{15}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Gọi \(A\) là biến cố “Chọn được một học sinh nam”.
Gọi \(B\) là biến cố “Chọn được một học sinh đạt điểm giỏi môn Toán”.
\(A \cap B\) là biến cố “Chọn được một học sinh đạt điểm giỏi môn Toán biết học sinh đó là học sinh nam”.
Ta có \(P\left( {A \cap B} \right) = \frac{{10}}{{45}} = \frac{2}{9}\); \(P\left( A \right) = \frac{{20}}{{45}} = \frac{4}{9}\).
\(P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{1}{2}\).
Vậy xác suất để giáo viên chọn được một học sinh đạt điểm giỏi môn Toán biết học sinh đó là học sinh nam là \(\frac{1}{2}\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giả sử \(T\) là biến cố “ Gặp sinh viên thi trượt môn Toán”, có \(P\left( T \right) = 0,3\).
\(L\) là biến cố “Gặp sinh viên thi trượt môn Tâm lý”, có \(P\left( L \right) = 0,22\). Khi đó \(P\left( {L|T} \right) = 0,4\).
Sơ đồ hình cây:
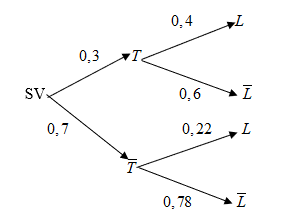
a) Sai. Vì xác suất gặp sinh viên thi trượt cả môn Toán và Tâm Lý là:
\(P\left( {TL} \right) = P\left( T \right)P\left( {L|T} \right) = 0,3.0,4 = 0,12\).
b) Đúng. Xác suất gặp sinh viên đậu cả môn Toán và Tâm lý là
\(P\left( {\overline {TL} } \right) = 1 - P\left( {T \cup L} \right) = 1 - P\left( T \right) - P\left( L \right) + P\left( {TL} \right) = 1 - 0,3 - 0,22 + 0,12 = 0,6\).
c) Sai. Xác suất gặp sinh viên đậu môn Toán, biết rằng sinh viên này trượt môn Tâm lý là
\(P\left( {\overline T |L} \right) = \frac{{P\left( {\overline T L} \right)}}{{P\left( L \right)}} = \frac{{P\left( L \right) - P\left( {TL} \right)}}{{P\left( L \right)}} = \frac{{0,22 - 0,12}}{{0,22}} = 0,45\).
d) Đúng. Theo công thức tính xác suất toàn phần, xác suất gặp sinh viên đậu môn Tâm lý là
\(P\left( {\overline L } \right) = P\left( T \right).P\left( {\overline L |T} \right) + P\left( {\overline T } \right).P\left( {\overline L |\overline T } \right) = 0,3.0,6 + 0,7.0,78 = 0,726\).
Câu 2
A. \(3\).
B. \(2\)
C. \(4\).
D. \(1\).
Lời giải
Chọn A
Tập hợp các kết quả thuận lợi cho biến cố \(A\)là \(\left\{ {\left( {3;1} \right),\left( {3;2} \right),\left( {3;4} \right)} \right\}\).
Vậy \(n\left( A \right) = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\frac{1}{4}\].
B. \[0,86\].
C. \[\frac{{30}}{{43}}\].
D. \[\frac{{25}}{{86}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{3}{{20}}\).
B. \(\frac{4}{5}\).
C. \(\frac{1}{5}\).
D. \(\frac{3}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[0,35\].
B. \[0,3\].
C. \[0,65\].
D. \[0,55\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo