Một cửa hàng dành tối đa 10 triệu để nhập \(x\) tạ gạo và \(y\) tạ mì. Biết mỗi tạ gạo mua hết 1,5 triệu, mỗi tạ mì mua hết 1,2 triệu. Khi đó:

a) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) là: \(1,5x + 1,2y \le 10\).

b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) là: \(1,5x + 1,2y \ge 10\).

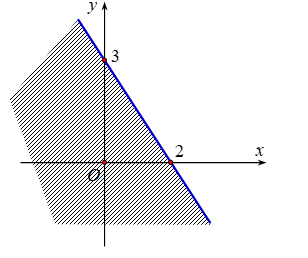
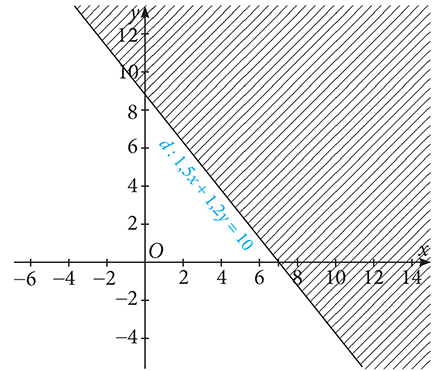
c) Miền nghiệm của bất phương trình \(1,5x + 1,2y \le 10\) là nửa mặt phẳng bờ là đường thẳng \(d:1,5x + 1,2y = 10\) chứa điểm \(O(0;0)\)

d) Miền nghiệm của bất phương trình \(1,5x + 1,2y \le 10\) là nửa mặt phẳng bờ là đường thẳng \(d:1,5x + 1,2y = 10\) không chứa điểm \(O(0;0)\)

Gọi \(x,y(xe)\) lần lượt là số xe loại \(A\) và \(B\) cần thuê.

Khi đó, số tiền cần bỏ ra để thuê xe là \(F(x;y) = 5x + 4y\) (triệu đồng)

Ta có \(x\) xe loại \(A\) chở được \(30x\) người và \(0,8x\) tấn hàng; \(y\) xe loại \(B\) chở được \(20y\) người và \(1,6y\) tấn hàng.

Suy ra \(x\) xe loại \(A\) và \(y\) xe loại \(B\) chở được \(30x + 20y\) người và \(0,8x + 1,6y\) tấn hàng.

Ta có hệ bất phương trình sau: \(\left\{ {\begin{array}{*{20}{l}}{30x + 20y \ge 180}\\{0,8x + 1,6y \ge 8}\\{0 \le x \le 10}\\{0 \le y \le 9}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + 2y \ge 18}\\{x + 2y \ge 10}\\{0 \le x \le 10}\\{0 \le y \le 9}\end{array}} \right.} \right.\) (*)

Bài toán trở thành tìm giá trị nhỏ nhất của \(F(x;y)\) trên miền nghiệm của hệ (*).

Miền nghiệm của hệ \((*)\) là tứ giác \(ABCD\) (kể cả bờ)

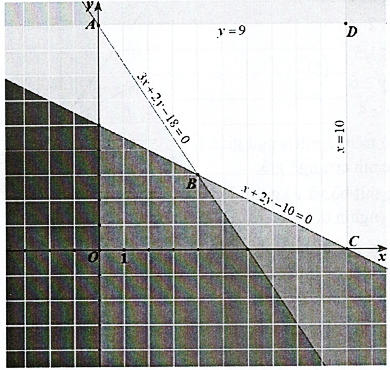
Tìm tọa độ các điểm \(A,B,C,D\).

Tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y - 18 = 0}\\{y = 9}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 9}\end{array}} \right.} \right.\). Vậy \(A(0;9)\).

Tọa độ điểm \(B\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{3x + 2y - 18 = 0}\\{x + 2y - 10 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = 3}\end{array}} \right.} \right.\). Vậy \(B(4;3)\).

Tọa độ điểm \(C\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 10}\\{x + 2y - 10 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 10}\\{y = 0}\end{array}} \right.} \right.\). Vậy \(C(10;0)\).

Tọa độ điểm \(D\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 10}\\{y = 9}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 10}\\{y = 9}\end{array}} \right.} \right.\). Vậy \(D(10;9)\).

Ta thấy \(F(x;y) = 5x + 4y\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A,B,C,D\).

Tại \(A(0;9)\) thì \(F = 36\) (triệu đồng).

Tại \(B(4;3)\) thì \(F = 32\) (triệu đồng).

Tại \(C(10;0)\) thì \(F = 50\) (triệu đồng).

Tại \(D(10;9)\) thì \(F = 86\) (triệu đồng).

Như vậy để chi phí thấp nhất cần thuê 4 xe loại \(A\) và 3 xe loại \(B\).

Tìm giá trị lớn nhất của biểu thức \(F = x - 3y + 1\) trên miền xác định bởi hệ

\(\left\{ {\begin{array}{*{20}{l}}{2x - y \le 4}\\{y - x \le 1}\\{x + y \ge 2}\end{array}} \right.\)

Vẽ đường thẳng \({d_1}:2x - y - 4 = 0\) đi qua hai điểm \((0; - 4)\) và \((2;0)\).

Vẽ đường thẳng \({d_2}: - x + y - 1 = 0\) đi qua hai điểm \((0;1)\) và \(( - 1;0)\).

Vẽ đường thẳng \({d_3}:x + y - 2 = 0\) đi qua hai điểm \((0;2)\) và \((2;0)\).

Xét điểm \(M(2;2)\). Ta thấy tọa độ \(M\) thỏa mãn tất cả các bất phương trình trong hệ.

Do đó, miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y \le 4}\\{y - x \le 1}\\{x + y \ge 2}\end{array}} \right.\) là miền không bị tô đậm (hình tam giác \(ABC\) bao gồm cả các cạnh \(AB,BC\) và \(AC\) trên hình vẽ).

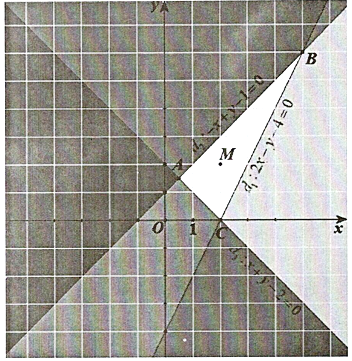
Tìm tọa độ các điểm \(A,B,C\).

Điểm \(A = {d_2} \cap {d_3}\) nên tọa độ điểm \(A\) là

nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{ - x + y = 1}\\{x + y = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{1}{?}}\\{y = \frac{3}{2}}\end{array}} \right.} \right.\).

Vậy \(A\left( {\frac{1}{2};\frac{3}{2}} \right)\).

Điểm \(B = {d_1} \cap {d_2}\) nên tọa độ điềm \(B\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{2x - y - 4 = 0}\\{ - x + y - 1 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5}\\{y = 6}\end{array}} \right.} \right.\). Vậy \(B(5;6)\).

Điểm \(C = {d_1} \cap {d_3}\) nên tọa độ điểm \(C\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{2x - y - 4 = 0}\\{x + y - 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 0}\end{array}} \right.} \right.\). Vậy \(C(2;0)\).

Ta thấy \(F = x - 3y + 1\) đạt giá trị lớn nhất chỉ có thể tại các điểm \(A,B,C\).

Tại \(A\left( {\frac{1}{2};\frac{3}{2}} \right)\) thì \(F = - 3\).

Tại \(B(5;6)\) thì \(F = - 12\)

Tại \(C(2;0)\) thì \(F = 3\)

Vậy giá trị lớn nhất của biểu thức \(F = x - 3y + 1\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{l}}{2x - y \le 4}\\{y - x \le 1{\rm{ l\`a }}3}\\{x + y \ge 2}\end{array}} \right.\)

 khi \(x = 2,y = 0\).