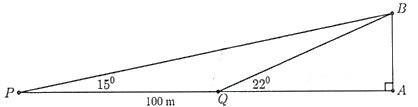
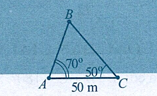
Cho tam giác ABC có \[BC = 10\] và góc\[A = {30^0}\]. Bán kính \[R\] của đường tròn ngoại tiếp tam giác ABC bằng
Quảng cáo
Trả lời:
Chọn D
Áp dụng định lý sin trong tam giác \[ABC\] ta có
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì \(ABCD\) là hình bình hành nên ta có:
Áp dụng định lí côsin cho tam giác \(ABC\), ta có:
Lời giải
Ta có: \({h_a} = \sqrt {p(p - a)} \Leftrightarrow \frac{{2S}}{a} = \sqrt {p(p - a)} \)
\(\begin{array}{l} \Leftrightarrow \frac{{2\sqrt {p(p - a)(p - b)(p - c)} }}{a} = \sqrt {p(p - a)} \Leftrightarrow 4(p - b)(p - c) = {a^2} \Leftrightarrow (a + c - b)(a + b - c) = {a^2}\\ \Leftrightarrow {a^2} - {(b - c)^2} = {a^2} \Leftrightarrow {(b - c)^2} = 0 \Leftrightarrow b = c.\end{array}\)
Vậy tam giác \(ABC\) cân tại \(A\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.