Trong không gian với hệ trục tọa độ \(Oxyz\), có hai trục \(Ox,\;Oy\) đặt trên mặt đất (coi mặt đất là một mặt phẳng); tia \(Oz\) hướng lên phía trên; đơn vị trên các trục tính bằng mét. Một thiết bị phát sóng \(M\)đặt tại điểm  \(A\left( {80;60;60} \right)\).  Vùng phủ sóng của thiết bị \(M\) có bán kính \(500\) mét. Gọi \(d\) là đường thẳng đi qua điểm \(B\left( {0; - 490;0} \right)\) và song song với trục \(Ox.\)

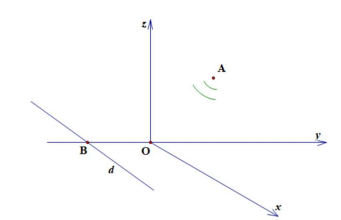
a) Một thiết bị thu sóng \(N\)(coi như một điểm) di chuyển trên trục \(Oy\)từ vị trí \(B\) theo hướng của vectơ \(\overrightarrow {BO} \). Thiết bị thu sóng \(N\)phải di chuyển một đoạn đường ngắn nhất bằng \[60,3\]mét thì vào được vùng phủ sóng của thiết bị \[M\].

b) Điểm \[B\] không thuộc vùng phủ sóng của thiết bị \[M\].

c) Một thiết bị thu sóng \(N\)(coi như một điểm) di chuyển trên đường thẳng  \(d\) thì có thể vào được vùng phủ sóng của thiết bị \[M\].

d) Phương trình tham số của đường thẳng  \(d\) là  \[\left\{ \begin{array}{l}x = 0\\y =  - 490\\z = t\end{array} \right.\left( {t \in \mathbb{R}} \right)\].

Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định chính xác vị trí của một vật trong không gian. Cách thức hoạt động của GPS như sau: Trong cùng một thời điểm, vị trí \(M\) của một vật sẽ được xác định bằng 4 vệ tinh cho trước, các vệ tinh này có gắn máy thu tín hiệu, bằng cách so sánh thời gian từ lúc tín hiệu được phát đi với thời gian nhận tín hiệu phản hồi thì sẽ xác định được khoảng cách từ các vệ tinh đến vị trí \(M\). Như vậy, vị trí \(M\) là giao điểm của 4 mặt cầu có tâm là 4 vệ tinh đã cho. Giả sử trong không gian \(Oxyz\), 4 vệ tinh có tọa độ là\(A\left( { - 1;6;3} \right)\), \(B\left( {4;8;1} \right)\), \(C\left( {9;6;7} \right)\), \(D\left( { - 15;18;7} \right)\). Biết khoảng cách từ \(M\) đến các vệ tinh lần lượt là \(MA = 6\), \(MB = 7\), \(MC = 12\), \(MD = 24\). Khi đó tọa độ điểm \(M\left( {{x_M};\,{y_M};\,{z_M}} \right)\). Tính giá trị biểu thức \(T = {x_M} + {y_M} + {z_M}\).

Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1\,;\,1\,;\,2} \right)\) và \(B\left( {3\,;\,1\,;\,0} \right)\). Mặt cầu đường kính \(AB\) có phương trình là

Trong không gian \(Oxyz\), một cabin cáp treo ở Bà Nà Hill xuất phát từ điểm \(A\left( { - 2;1;5} \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\vec u\left( {0; - 2;6} \right)\) với tốc độ là \(4\,{\rm{m/s}}\) (đơn vị trên mỗi trục toạ độ là mét). Sau \(5\) giây kể từ lúc xuất phát, cabin đến điểm \(M\). Gọi tọa độ \(M\left( {a;b;c} \right)\). Tính \(a + 3b + c\).

Với hệ trục tọa độ \(Oxyz\) sao cho \(O\) nằm trên mặt nước, mặt phẳng \(\left( {Oxy} \right)\) là mặt nước, trục \(Oz\) hướng lên trên (đơn vị đo: mét), một con chim bói cá đang săn mồi ở vị trí \[C\] cách mặt nước \[5\,\,{\rm{m}}{\rm{,}}\] cách mặt phẳng \(\left( {Oxz} \right),\left( {Oyz} \right)\) lần lượt là \(6\,\,{\rm{m}}\) và \(2\,{\rm{m}}\), từ vị trí này nó phóng thẳng xuống vị trí con cá ở vị trí \[A\], biết con cá cách mặt nước \(50\,\,{\rm{cm}}{\rm{,}}\)cách mặt phẳng \(\left( {Oxz} \right),\left( {Oyz} \right)\) lần lượt là \(1\,{\rm{m}}\) và \(1,5\,{\rm{m}}\) (tham khảo hình vẽ).

Giả sử vận tốc của con chim bói cá là \(4\,\,{\rm{m/s}}\), hỏi sau bao nhiêu giây thì nó chạm tới mặt nước (làm tròn đến hàng phần trăm)?

Trong không gian với hệ tọa độ \[Oxyz\] (đơn vị trên mỗi trục là kilomet), một trạm phát sóng radar của Nga được đặt trên bán đảo Crimea ở vị trí \(I\left( { - 2;1; - 1} \right)\) và được thiết kế phát hiện máy bay của địch ở khoảng cách tối đa \(500\) kilomet.

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phát sóng của radar trong không gian?

b) Hai chiếc máy bay do thám của Mỹ và Anh đang bay ở vị trí có tọa độ \(M\left( { - 200;100; - 250} \right)\) và \(N\left( {350; - 100;300} \right)\). Hỏi hai chiếc máy bay đó có bị radar phát hiện hay không?

Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(I\left( {1;0; - 1} \right)\) và \(A\left( {2;2; - 3} \right)\). Mặt cầu \(\left( S \right)\) tâm \(I\) và đi qua điểm \(A\) có phương trình là

Manhattanhenge (Hình 1) là một sự kiện diễn ra khi Mặt Trời mọc hoặc khi Mặt Trời lặn nằm thẳng hàng với các tuyến phố Đông - Tây thuộc mạng lưới đường phố chính tại quận Manhattan của thành phố New York. Khi mặt trời lặn, tia sáng song song mặt đất lệch một góc khoảng \(38^\circ \) so với hướng tây (Hình 2).

Giả sử mặt tiền các tòa nhà hai bên đường nằm trong 2 mặt phẳng song song cách nhau \(30\)m và vuông góc với mặt đất. Biết rằng mặt phẳng phía bắc đi qua gốc \(O\) của hệ trục \(Oxyz\), với tia \(Oz\) vuông góc với mặt đất và hướng lên trên. Phương trình mặt phẳng thứ hai có dạng \(\left( Q \right):x + ay + bz + c = 0\) với \(c = \frac{m}{{\sin n^\circ }}\). Tính \(m + n\).