20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 14. Phương trình mặt phẳng có đáp án
90 người thi tuần này 4.6 1.2 K lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \[\overrightarrow {AC} .\]
B. \[\overrightarrow {AC'} .\]
C. \[\overrightarrow {AA'} .\]
D. \[\overrightarrow {AD'} .\]
Lời giải
Đáp án đúng là: C
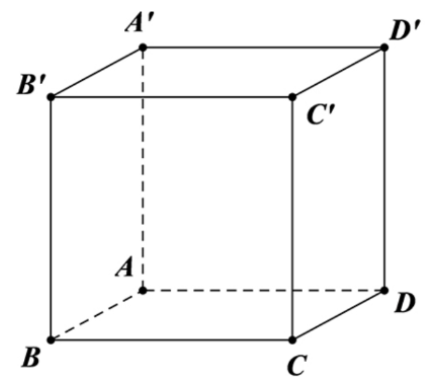
Ta có: \[ABCD.A'B'C'D'\] là hình lập phương nên \[\overrightarrow {AA'} \bot \left( {ABCD} \right)\].
Do đó, \[\overrightarrow {AA'} \] là vectơ pháp tuyến của mặt phẳng \[\left( {ABCD} \right)\].
Câu 2
A. \[{x^2} + 2y + z - 3 = 0.\]
B. \[{x^2} + {y^2} + {z^2} - 2 = 0.\]
C. \[{x^2} + 2{y^2} + z - 5 = 0.\]
D. \[x + 2y + z - 4 = 0.\]
Lời giải
Đáp án đúng là: D
Phương trình tổng quát của mặt phẳng có dạng: \[ax + by + cz + d = 0\] trong đó \[a,b,c\] không đồng thời bằng 0.
Do đó, ta chọn D.
Câu 3
A. \[A\left( { - 1; - 1; - 1} \right).\]
B. \[B\left( {1;1;1} \right).\]
C. \[C\left( {1;1; - 1} \right).\]
D. \[D\left( { - 3;0;0} \right).\]
Lời giải
Đáp án đúng là: B
Thay tọa độ vào phương trình mặt phẳng, ta có:
Với điểm \[A\left( { - 1; - 1; - 1} \right),\] ta được: \[ - 1 + \left( { - 1} \right) + \left( { - 1} \right) - 3 = - 6 \ne 0.\]
Do đó, mặt phẳng \[\left( P \right)\] không đi qua điểm \[A\left( { - 1; - 1; - 1} \right).\]
Với điểm \[B\left( {1;1;1} \right)\], ta được: \[1 + 1 + 1 - 3 = 0\].
Do đó, mặt phẳng \[\left( P \right)\] đi qua điểm \[B\left( {1;1;1} \right).\]
Với điểm \[C\left( {1;1; - 1} \right),\] ta được: \[1 + 1 + \left( { - 1} \right) - 3 = - 2 \ne 0.\]
Do đó, mặt phẳng \[\left( P \right)\] không đi qua điểm \[C\left( {1;1; - 1} \right).\]
Với điểm \[D\left( { - 3;0;0} \right)\], ta được: \[ - 3 + 0 + 0 - 3 = - 6 \ne 0.\]
Do đó, mặt phẳng \[\left( P \right)\] không đi qua điểm \[D\left( { - 3;0;0} \right).\]
Câu 4
A. \[\overrightarrow n = \left( {2;1;1} \right).\]
B. \[\overrightarrow n = \left( { - 2;1; - 1} \right).\]
C. \[\overrightarrow n = \left( {2; - 1; - 1} \right).\]
D. \[\overrightarrow n = \left( {1;1;1} \right).\]
Lời giải
Đáp án đúng là: A
Vectơ pháp tuyến của mặt phẳng \[\left( \alpha \right):2x + y + z + 1 = 0\] là \[\overrightarrow n = \left( {2;1;1} \right).\]
Câu 5
A. \[P\left( {0;2;0} \right).\]
B. \[Q\left( {0;0;3} \right).\]
C. \[M\left( {1;2;3} \right).\]
D. \[N\left( {1;0;0} \right).\]
Lời giải
Đáp án đúng là: C
Xét các đáp án, ta thấy điểm \[M\left( {1;2;3} \right)\] không thuộc mặt phẳng \[\left( P \right)\] do
\[\frac{1}{1} + \frac{2}{2} + \frac{3}{3} = 3 \ne 1.\]
Câu 6
A. \[2x + 3y - z - 2 = 0.\]
B. \[2x + 3y - z + 2 = 0.\]
C. \[2x - y + 3z - 2 = 0.\]
D. \[2x - y + 3z + 2 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\overrightarrow n = \left( {2;1;2} \right).\]
B. \[\overrightarrow n = \left( {2; - 1; - 2} \right).\]
C. \[\overrightarrow n = \left( {2;1; - 2} \right).\]
D. \[\overrightarrow n = \left( { - 2;1; - 2} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[2x - 3y + 6z + 12 = 0.\]
B. \[2x - 3y - 6z - 12 = 0.\]
C. \[2x - 3y + 6z = 0.\]
D. \[2x + 3y + 6z + 12 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1.\]
B. \[ - \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1.\]
C. \[\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0.\]
D. \[\frac{x}{1} - \frac{y}{2} + \frac{z}{3} = 1.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[ - \frac{5}{3}.\]
B. \[\frac{7}{3}.\]
C. \[\frac{5}{3}.\]
D. \[5.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[\left( P \right):x + y + 2z - 3 = 0.\]
B. \[\left( P \right):x + y + 2z - 6 = 0.\]
C. \[\left( P \right):x + 3y + 4z - 7 = 0.\]
D. \[\left( P \right):x + 3y + 4z - 26 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[2x - y - 2z = 0.\]
B. \[2x + y - 2z = 0.\]
C. \[2x - y + 2z = 0.\]
D. \[2x + y - 2z + 1 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \[2x + y + 3z + 7 = 0.\]
B. \[2x + y - 3z + 7 = 0.\]
C. \[2x - y + 3z + 7 = 0.\]
D. \[2x - y + 3z - 7 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[\frac{7}{{\sqrt {14} }}.\]
B. \[\frac{8}{{\sqrt {14} }}.\]
C. \[\frac{5}{{\sqrt {14} }}.\]
D. \[14.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \[m = n = - 4.\]
B. \[m = 4;n = - 4.\]
C. \[m = - 4;n = 4.\]
D. \[m = n = 4.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \[S = 12.\]
B. \[S = - 12.\]
C. \[S = 0.\]
D. \[S = - 24.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \[4x - 2y - z + 4 = 0.\]
B. \[4x + 2y - z - 4 = 0.\]
C. \[4x + 2y + z + 4 = 0.\]
D. \[4x - 2y - z - 4 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. \[4.\]
B. \[\sqrt 2 .\]
C. \[2\sqrt 2 .\]
D. \[8.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.