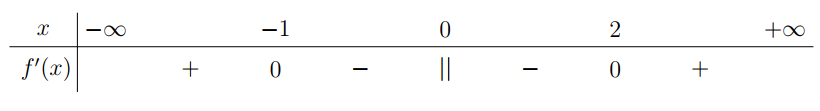12 bài tập Sử dụng dấu của đạo hàm để tìm khoảng đồng biến, nghịch biến của hàm số có lời giải
134 người thi tuần này 4.6 1.7 K lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 1
274 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 9
253 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 8
253 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 7
250 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 6
254 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 5
254 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 4
253 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 3
262 lượt thi
22 câu hỏi
Danh sách câu hỏi:
Câu 1
A. (1; +∞);
B. (−∞; 1);
C. (−1; +∞);
D. (−∞; −1).
Lời giải
Đáp án đúng là: D
Từ bảng xét dấu ta thấy hàm số đã cho nghịch biến trên khoảng (−∞; −1) và (−1; 1).
Vậy hàm số đã cho nghịch biến trên khoảng (−∞; −1).
Câu 2
A. (−∞; 0);
B. (2; +∞);
C. (0; +∞);
D. (−1; 2).
Lời giải
Đáp án đúng là: B
Dựa vào bảng xét dấu, ta thấy hàm số đồng biến trên khoảng (2; +∞).
Câu 3
A. \(y = \frac{{x - 1}}{{x - 2}}\);
B. y = x3 + x;
C. y = −x3 – 3x;
D. \(y = \frac{{x + 1}}{{x + 3}}\).
Lời giải
Đáp án đúng là: B
y = x3 + x y' = 3x2 + 1 > 0, ∀x ∈ ℝ.
Câu 4
A. Hàm số nghịch biến trên khoảng (−∞; +∞);
B. Hàm số nghịch biến trên khoảng (−1; +∞);
C. Hàm số nghịch biến trên khoảng (−∞; −1);
D. Hàm số đồng biến trên khoảng (−∞; −1).
Lời giải
Đáp án đúng là: D
Tập xác định: ℝ\{−1}.
Ta có \[y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}} > 0\], ∀x ∈ ℝ\{−1}.
Câu 5
A. y = x4 + 3x2;
B. \(y = \frac{{x - 2}}{{x + 1}}\);
C. y = 3x3 + 3x – 2;
D. y = 2x3 – 5x + 1.
Lời giải
Đáp án đúng là: C
Hàm số y = 3x3 + 3x – 2 có tập xác định D = ℝ.
Có y' = 27x2 + 3 > 0, ∀x ∈ ℝ, suy ra hàm số đồng biến trên khoảng (−∞; +∞).
Câu 6
A. (−∞; +∞);
B. (0; +∞);
C. (−∞; 0);
D. (−1; 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hàm số đồng biến trên khoảng (0; +∞);
B. Hàm số đồng biến trên khoảng (−∞; 0);
C. Hàm số nghịch biến trên khoảng (0; +∞);
D. Hàm số nghịch biến trên khoảng (−1; 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. (−∞; 1);
B. (−∞; −1);
C. (1; 3);
D. (3; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. (1010; 2018);
B. (2018; +∞);
C. (0; 1009);
D. (1; 2018).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập