12 bài tập Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn có lời giải
41 người thi tuần này 4.6 0.9 K lượt thi 12 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
a) Với 0 ≤ t ≤ 12 ta có:
N'(t) = −3t2 + 24t, N'(t) = 0 −3t2 + 24t = 0 t = 0 (tm) hoặc t = 8 (tm).
Ta có: N(0) = 0, N(8) = 256; N(12) = 0.
Do đó, số người tối đa bị nhiễm bệnh ở địa phương là 256 người trong 12 tuần đầu.
b) Hàm số biểu thị tốc độ độ lây lan của virus là: N'(t) = −3t2 + 24t.
Đặt f(t) = −3t2 + 24t, 0 ≤ t 12.
Ta có: f'(t) = −6t + 24, f'(t) = 0 t = 4 (tm).
Có f(0) = 0, f(4) = −3.42 + 24.4 = 48, f(12) = −3.122 + 14.12 = −144.
Do đó, virus sẽ lây lan nhanh nhất khi t = 4 (tuần thứ 4).
Lời giải
Hướng dẫn giải:
a) Ta có: \(p = 15 - \frac{1}{2}q \Leftrightarrow q = 2(15 - p)\).
Thay vào R = pq ta được: R = p.2.(15 – p) = −2p2 + 30p.
b) Đặt y = −2p2 + 30p.
Tập xác định: D = (0; +∞).
Có y' = −4p + 30 = 0 p = 7,5.
Bảng biến thiên:
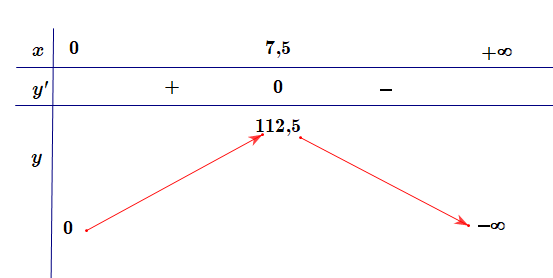
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D y = y(7,5) = 112,5\).
Vậy nếu giá bán mỗi kilôgam sản phẩm là 7,5 nghìn đồng/kg thì sẽ đạt được doanh thu cao nhất là 112,5 nghìn đồng.
Câu 3
A. 1s;
B. 3s;
C. 2s;
D. 4s.
Lời giải
Đáp án đúng là: D
Ta có v(t) = s'(t) = −3t2 + 12t.
Có v(t) = 0 −3t2 + 12t = 0 t = 0 hoặc t = 4.
Vậy tại thời điểm t = 4 s thì vận tốc của chất điểm bằng 0.
Câu 4
A. 14 (m/s2);
B. 12 (m/s2);
C. 13 (m/s2);
D. 11 (m/s2);
Lời giải
Đáp án đúng là: A
Có v(t) = S'(t) = 3t2 +8t; a(t) = v'(t) = 6t + 8.
Thời điểm vận tốc bằng 11 m/s ứng với 3t2 +8t = 11 t = 1 (giây).
Gia tốc của vật cần tìm là a(1) = 6 + 8 =14 (m/s2).
Câu 5
A. 289 m/s.
B. 105 m/s.
C. 111 m/s.
D. 487 m/s.
Lời giải
Đáp án đúng là: B
Ta có v(t) = s' = −6t2 + 48t +9.
Xét hàm số v(t) = −6t2 + 48t +9, t [0; 10].
Ta có v'(t) = −12t + 48 = 0 t = 4 (thỏa mãn).
Ta có v(0) = 9; v(4) = 105; v(10) = −111 \( \Rightarrow \mathop {\max }\limits_{\left[ {0;10} \right]} v\left( t \right) = v\left( 4 \right) = 105\).
Câu 6
A. Vận tốc của vật tại thời điểm t = 3 giây là v(3) = 1 m/s;
B. Quãng đường vật đi được từ lúc bắt đầu chuyển động đến khi vật đứng yên là 162 m;
C. Gia tốc của vật tại thời điểm t = 3 giây là a(3) = 2 m/s2;
D. Trong 9 giây đầu tiên, vật tăng vận tốc khi t [0; 4].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Dân số của quốc gia vào năm 2030 là: 108,763 (triệu người);
B. Dân số của quốc gia vào năm 2035 là: 125,488 (triệu người);
C. Xem N(t) là hàm số của biến số t xác định trên đoạn [0; 50]. Khi đó hàm số N(t) đồng biến trên đoạn [0; 50];
D. Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vậy vào năm 2046 thì tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 1418000 đồng.
B. 1403000 đồng.
C. 1402000 đồng.
D. 1417000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 40
phút;
B. 44 phút;
C. 30 phút;
D. 38 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. Ngay từ lúc bắt đầu sử dụng độc tố;
B. Sau 0,5 giờ;
C. Sau 2 giờ;
D. Sau 1 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 60;
B. 45;
C. 30;
D. 25.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.