Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số N(t) = −t3 + 12t2, 0 ≤ t ≤ 12, trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
b) Đạo hàm N'(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Quảng cáo
Trả lời:
Hướng dẫn giải:
a) Với 0 ≤ t ≤ 12 ta có:
N'(t) = −3t2 + 24t, N'(t) = 0 −3t2 + 24t = 0 t = 0 (tm) hoặc t = 8 (tm).
Ta có: N(0) = 0, N(8) = 256; N(12) = 0.
Do đó, số người tối đa bị nhiễm bệnh ở địa phương là 256 người trong 12 tuần đầu.
b) Hàm số biểu thị tốc độ độ lây lan của virus là: N'(t) = −3t2 + 24t.
Đặt f(t) = −3t2 + 24t, 0 ≤ t 12.
Ta có: f'(t) = −6t + 24, f'(t) = 0 t = 4 (tm).
Có f(0) = 0, f(4) = −3.42 + 24.4 = 48, f(12) = −3.122 + 14.12 = −144.
Do đó, virus sẽ lây lan nhanh nhất khi t = 4 (tuần thứ 4).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 40
phút;
B. 44 phút;
C. 30 phút;
D. 38 phút.
Lời giải
Đáp án đúng là: A
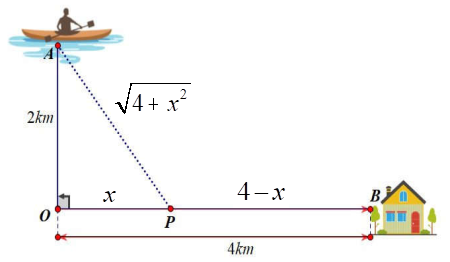
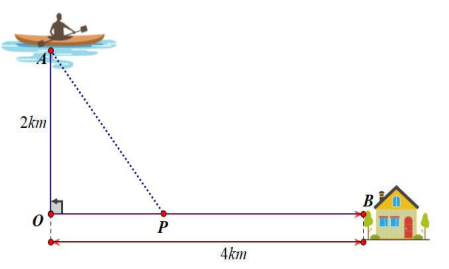
Đặt OP = x (0 < x < 4) BP = 4 – x; \(AP = \sqrt {4 + {x^2}} \).
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm B là:
\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}\,\,\left( h \right)\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}\).
\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}} = 5x \Leftrightarrow \left\{ \begin{array}{l}0 < x < 4\\4{x^2} = 9\end{array} \right. \Leftrightarrow x = \frac{3}{2}.\)
Bảng biến thiên
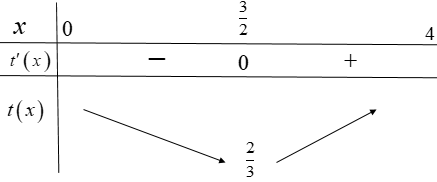
Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm B là: \({t_{\min }} = \frac{2}{3}\,\left( h \right)\, = \frac{2}{3}.60\,\left( {ph\'u t} \right) = 40\,ph\'u t.\)
</></>
Câu 2
A. 1418000 đồng.
B. 1403000 đồng.
C. 1402000 đồng.
D. 1417000 đồng.
Lời giải
Đáp án đúng là: C
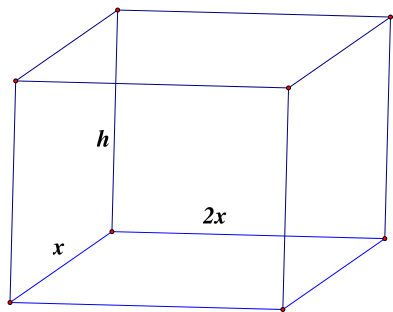
Gọi x là chiều rộng của đáy thùng, x > 0, đơn vị m.
chiều dài của đáy thùng là: 2x.
Ta có V = x.2x.h = 10 \(h = \frac{5}{{{x^2}}}\).
Chi phí làm đáy thùng là: 2x2.75 = 150x2 (đơn vị nghìn đồng).
Chi phí làm diện tích xung quanh là : \(\left( {2x.\frac{5}{{{x^2}}} + 2.2x.\frac{5}{{{x^2}}}} \right).55 = \frac{{1650}}{x}\) (đơn vị nghìn đồng).
Chi phí làm thùng là : \(T = 150{x^2} + \frac{{1650}}{x}\) (đơn vị nghìn đồng).
Xét hàm số \(T = 150{x^2} + \frac{{1650}}{x}\), với x > 0.
Ta có \(T'\left( x \right) = 300x - \frac{{1650}}{{{x^2}}}\) ; \(T'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{\frac{{11}}{2}}}\).
Bảng biến thiên
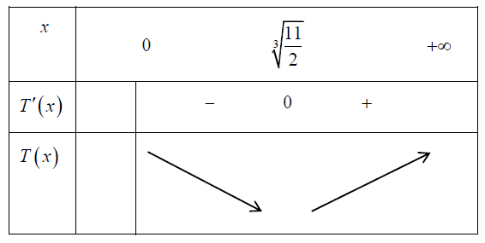
Dựa vào bảng biến thiên T(x) đạt giá trị nhỏ nhất tại \(x = \sqrt[3]{{\frac{{11}}{2}}}\).
Vậy chi phí ít nhất bằng \(T = 150{\left( {\sqrt[3]{{\frac{{11}}{2}}}} \right)^2} + \frac{{1650}}{{\sqrt[3]{{\frac{{11}}{2}}}}} \approx 1402000\) đồng.
Câu 3
A. 289 m/s.
B. 105 m/s.
C. 111 m/s.
D. 487 m/s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Ngay từ lúc bắt đầu sử dụng độc tố;
B. Sau 0,5 giờ;
C. Sau 2 giờ;
D. Sau 1 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Dân số của quốc gia vào năm 2030 là: 108,763 (triệu người);
B. Dân số của quốc gia vào năm 2035 là: 125,488 (triệu người);
C. Xem N(t) là hàm số của biến số t xác định trên đoạn [0; 50]. Khi đó hàm số N(t) đồng biến trên đoạn [0; 50];
D. Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vậy vào năm 2046 thì tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.