12 bài tập Một số bài toán về đường tiệm cận của đồ thị hàm số có chứa tham số có lời giải

37 người thi tuần này 4.6 37 lượt thi 12 câu hỏi 60 phút

Đề số 1

🔥 Đề thi HOT:

1454 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

50.3 K lượt thi 126 câu hỏi

1255 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

52.2 K lượt thi 304 câu hỏi

1021 người thi tuần này

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

11.8 K lượt thi 35 câu hỏi

889 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

10.8 K lượt thi 20 câu hỏi

837 người thi tuần này

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

10.3 K lượt thi 25 câu hỏi

819 người thi tuần này

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

8.5 K lượt thi 20 câu hỏi

786 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

8.1 K lượt thi 15 câu hỏi

758 người thi tuần này

7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)

7.5 K lượt thi 7 câu hỏi

Nội dung liên quan:

20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 1: Tính đơn điệu và cực trị của hàm số có đáp án

1420 lượt thi

1 đề

12 bài tập Sử dụng dấu của đạo hàm để tìm khoảng đồng biến, nghịch biến của hàm số có lời giải

227 lượt thi

1 đề

12 bài tập Sử dụng đồ thị của hàm số f'(x) để tìm khoảng đồng biến, nghịch biến của hàm số f(x) số có lời giải

203 lượt thi

1 đề

12 bài tập Sử dụng bảng biến thiên, đồ thị hàm số để tìm khoảng đồng biến, nghịch biến của hàm số có lời giải

127 lượt thi

1 đề

12 bài tập Sử dụng dấu của đạo hàm để tìm điểm cực trị của hàm số có lời giải

120 lượt thi

1 đề

12 bài tập Sử dụng bảng biến thiên, đồ thị hàm số để tìm điểm cực trị của hàm số có lời giải

129 lượt thi

1 đề

12 bài tập Sử dụng đồ thị của hàm số f'(x) để tìm cực trị của hàm số f(x) có lời giải

132 lượt thi

1 đề

12 bài tập Một số bài toán thực tế ứng dụng tính đơn điệu và cực trị của hàm số có đáp án

180 lượt thi

1 đề

12 bài tập Một số bài toán liên quan đến tính đơn điệu, cực trị có chứa tham số có đáp án

117 lượt thi

1 đề

12 bài tập Một số bài toán hàm hợp liên quan đến tính đơn điệu và cực trị có đáp án

154 lượt thi

1 đề

Danh sách câu hỏi:

Câu 1:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \[y = \frac{{mx - 8}}{{x + 2}}\] có hai đường tiệm cận.

A. m ≠ 4;

B. m ≠ −4;

C. m = 4;

D. m = −4.

Câu 2:

Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}.\) Tìm a, b để đồ thị hàm số có x = 1 là tiệm cận đứng và \(y = \frac{1}{2}\) là tiệm cận ngang.

A. a = −1; b = 2;

B. a = 4; b = 4;

C. a = 1; b = 2;

D. a = −1; b = −2.

Câu 3:

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận.

A. m = −1;

B. m ∈ {1; 4};

C. m = 4;

D. m ∈ {−1; −4}.

Câu 4:

Tìm tất cả giá trị của tham số m để đường tiệm cận xiên của đồ thị hàm số \(y = 2mx + 3 - \frac{4}{{x + 1}}\) đi qua điểm M(1; 7).

A. m = 1;

B. m = 3;

C. m = 2;

D. m = −2.

Câu 5:

Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (m, n là các số thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m + n.

A. 0;

B. −3;

C. 3;

D. 6.

Câu 6:

Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số \[y = \frac{{x - 1}}{{{x^2} - 8x + m}}\] có 3 đường tiệm cận?

A. 14;

B. 8;

C. 15;

D. 16.

Câu 7:

Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x₀, tiệm cận ngang là y = y₀ và x₀y₀ = 16. Hỏi m bằng?

A. m = 8;

B. m = −16;

C. m = 1;

D. m = 2.

Câu 8:

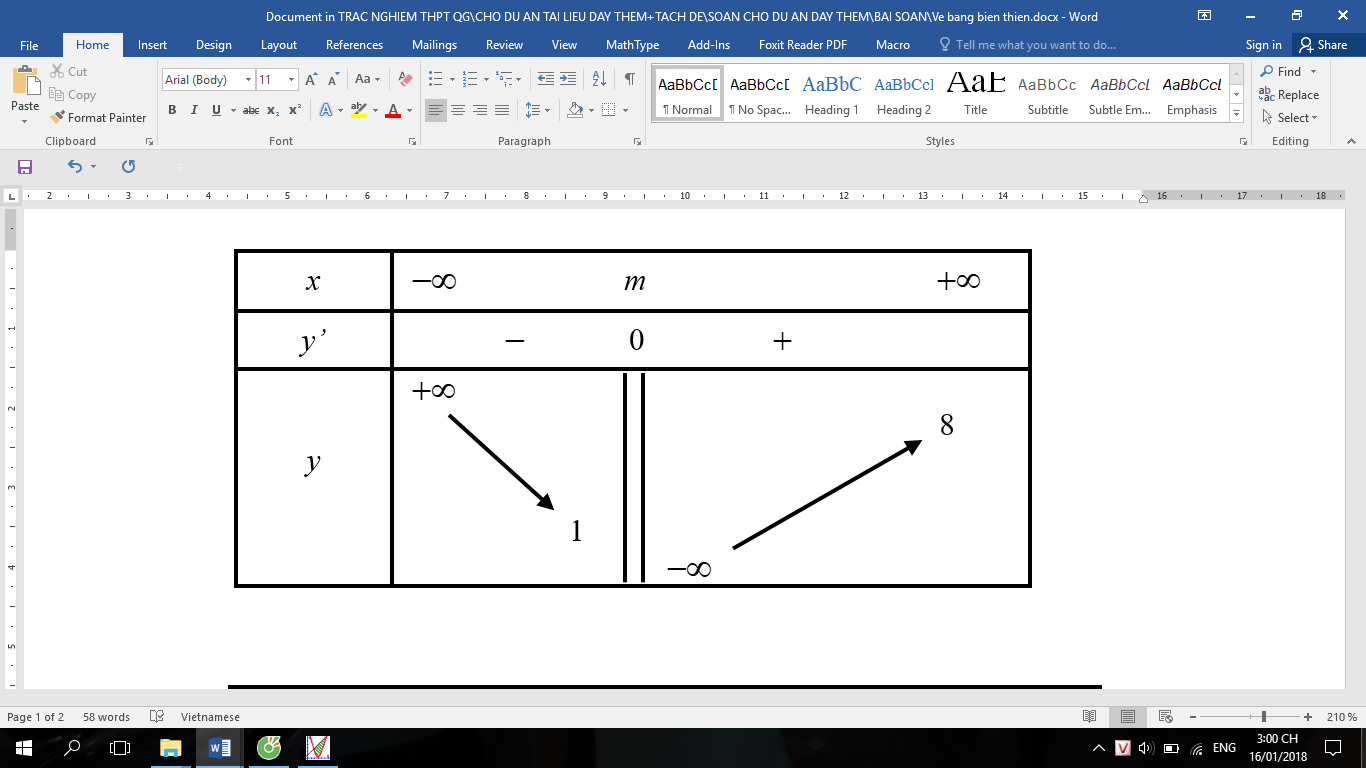
Cho hàm số y = f(x) có bảng biến thiên:

Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để hàm số có 4 tiệm cận?

A. 5;

B. 6;

C. 7;

D. 8.

Câu 9:

Cho hàm số y = f(x) có bảng biến thiên sau:

Tìm tổng số các giá trị nguyên dương của tham số m ∈ (−10; 10) để đồ thị hàm số y = f(x) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là 4.

A. 42;

B. 45;

C. −3;

D. 0.

Câu 10:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Định tham số m để giao điểm của đường tiệm cận đứng và tiệm cận ngang là điểm I(−1; 1).

A. Không có m;

B. m = 0;

C. m = −1;

D. m = 1.

Câu 11:

Tìm điều kiện của tham số m để đồ thị của hàm số \(y = \frac{{\left( {2m + 1} \right)x + 3}}{{x + 1}}\) có đường tiệm cận ngang đi qua điểm A(−2; 7).

Câu 12:

Cho hàm số \[y = f\left( x \right) = \frac{{nx + 1}}{{x + m}}\]; (mn ≠ 1) xác định trên ℝ\{−1}, liên tục trên từng khoảng xác định và có đồ thị như hình vẽ:

Tính tổng m + n.

4.6

7 Đánh giá

50%

40%

0%

0%

0%

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack