5 bài tập Bài toán tốc độ thay đổi của một đại lượng (có lời giải)
59 người thi tuần này 4.6 729 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc của vật là \(v = h'\left( t \right) = 24,5 - 9,8t\,\,\left( {{\rm{m}}/{\rm{s}}} \right)\).
Do đó, vận tốc của vật sau 2 giây là \(v\left( 2 \right) = 24,5 - 9,8.2 = 4,9\,\,\left( {{\rm{m}}/{\rm{s}}} \right)\).
b) Vì \(h\left( t \right)\) là hàm số bậc hai có hệ số \(a = - 4,9 < 0\) nên \(h\left( t \right)\) đạt giá trị lớn nhất tại
\(t = - \frac{b}{{2a}} = \frac{{24,5}}{{2 \cdot 4,9}} = 2,5\) (giây). Khi đó, độ cao lớn nhất của vật là \(h\left( {2,5} \right) = 32,625\,\,\left( m \right)\).
c) Vật chạm đất khi độ cao bằng 0 , tức là \(h = 2 + 24,5t - 4,9{t^2} = 0\) hay \(t \approx 5,08\) (giây).
Vận tốc của vật lúc chạm đât là \(v(\left( {5,08} \right)24,5 - 9,8 \cdot 5,08 = - 25,284\,\,\left( {{\rm{m}}/{\rm{s}}} \right)\).
Vận tốc âm chứng tỏ chiều chuyển động của vật là ngược chiều dương (hướng lên trên) của trục đã chọn (khi lập phương trình chuyển động của vật).
Lời giải
Ta có: \(P'\left( t \right) = \frac{{0,75a{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {b + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}},t \ge 0\).
Theo đề bài, ta có: \(P\left( 0 \right) = 20\) và \(P'\left( 0 \right) = 12\).
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\frac{a}{{b + 1}} = 20}\\{\frac{{0,75a}}{{{{\left( {b + 1} \right)}^2}}} = 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 20\left( {b + 1} \right)}\\{\frac{{15}}{{b + 1}} = 12.}\end{array}} \right.} \right.\)
Giải hệ phương trình này, ta được \(a = 25\) và \(b = \frac{1}{4}\).
Khi đó, \(P'\left( t \right) = \frac{{18,75{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {\frac{1}{4} + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}} > 0,\forall t \ge 0\), tức là số lượng quần thể nấm men luôn tăng.
Tuy nhiên, do \(\mathop {\lim }\limits_{t \to + \infty } P\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25}}{{\frac{1}{4} + {{\rm{e}}^{ - 0.75t}}}} = 100\) nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
Lời giải
a) Hàm chi phí biên là \(C'\left( x \right) = 300 - 5x + 0,375{x^2}\).
b) Ta có: \(C'\left( {200} \right) = 300 - 5 \cdot 200 + 0,375 \cdot {200^2} = 14300\).
Chi phí biên tại \(x = 200\) là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo (đơn vị hàng hoá thứ 201) là khoảng 14300 nghìn đồng.
c) Chi phí sản xuất đơn vị hàng hoá thứ 201 là
\(C\left( {201} \right) - C\left( {200} \right) = 1004372,625 - 990000 = 14372,625{\rm{ }}\)(nghìn đồng)
Giá trị này xấp xỉ với chi phí biên \(C'\left( {200} \right)\) đã tính ở câu trên.
Lời giải
Xét hàm số \(y = C\left( x \right) = \frac{{300x}}{{100 - x}},0 \le x < 100\).
Ta có:\(y' = \frac{{30000}}{{{{\left( {100 - x} \right)}^2}}} > 0\), với mọi \(x \in [0;100)\). Do đó hàm số luôn đồng biến trên nửa khoảng \(\left[ {0;100} \right)\) và\(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {{100}^ - }} \frac{{300x}}{{100 - x}} = + \infty \) nên đồ thị hàm số có tiệm cận đứng là \(x = 100\).
Bảng biến thiên:
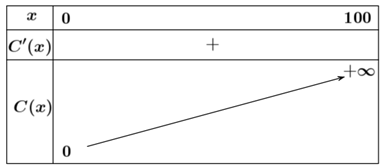
a) Chi phí cần bỏ ra \(C\left( x \right)\) sẽ luôn tăng khi \(x\) tăng.
b) Vì \(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = + \infty \) (hàm số \(C\left( x \right)\) không xác định khi \(x = 100)\) nên nhà máy không thể loại bỏ \(100\% \) chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa).
Lời giải
a) Tìm tốc độ phản ứng tại thời điểm \(t > 0\).
Tốc độ phản ứng là đạo hàm của \(\left[ C \right]\) theo biến \(t\)
Do đó \({\left[ C \right]^\prime } = {\left( {\frac{{{a^2}Kt}}{{aKt + 1}}} \right)^\prime } = \frac{{{a^2}K\left( {aKt + 1} \right) - {a^2}Kt.aK}}{{{{\left( {aKt + 1} \right)}^2}}} = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\)
b) Theo câu trên nếu \(x = \left[ C \right]\) thì \(x'\left( t \right) = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\)
Ta lại có \(K{\left( {a - x} \right)^2} = K{\left( {a - \frac{{{a^2}Kt}}{{aKt + 1}}} \right)^2} = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\) nên \(x'\left( t \right) = K{\left( {a - x} \right)^2}\)
c) Ta có \(\mathop {\lim }\limits_{x \to \infty } \left[ C \right] = \mathop {\lim }\limits_{x \to \infty } \left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}} = a\) (mol/l) nên nồng độ của chất \(C\) dần đến \(a\) (mol/l)
d) Ta có \(\mathop {\lim }\limits_{x \to \infty } x'\left( t \right) = \mathop {\lim }\limits_{x \to \infty } = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}} = 0\) (mol/l) nên tốc độ phản ứng dần đến \(0\).