Xét phản ứng hoá học tạo ra chất \(C\) từ hai chất \(A\) và \(B\): . Giả sử nồng độ của hai chất \(A\) và \(B\) bằng nhau \(\left[ A \right] = \left[ B \right] = a\) (mol/l) . Khi đó nồng độ của chất \(C\) theo thời gian \(t\) \(\left( {t > 0} \right)\) được cho bởi công thức: \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\)(mol/l) trong đó \(K\) là hằng số dương.
a) Tìm tốc độ phản ứng tại thời điểm \(t > 0\).
b) Chứng minh nếu \(x = \left[ C \right]\) thì \(x'\left( t \right) = K{\left( {a - x} \right)^2}\)
c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t \to + \infty \)
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t \to + \infty \)
Xét phản ứng hoá học tạo ra chất \(C\) từ hai chất \(A\) và \(B\): . Giả sử nồng độ của hai chất \(A\) và \(B\) bằng nhau \(\left[ A \right] = \left[ B \right] = a\) (mol/l) . Khi đó nồng độ của chất \(C\) theo thời gian \(t\) \(\left( {t > 0} \right)\) được cho bởi công thức: \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\)(mol/l) trong đó \(K\) là hằng số dương.
a) Tìm tốc độ phản ứng tại thời điểm \(t > 0\).
b) Chứng minh nếu \(x = \left[ C \right]\) thì \(x'\left( t \right) = K{\left( {a - x} \right)^2}\)
c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t \to + \infty \)
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t \to + \infty \)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tìm tốc độ phản ứng tại thời điểm \(t > 0\).
Tốc độ phản ứng là đạo hàm của \(\left[ C \right]\) theo biến \(t\)
Do đó \({\left[ C \right]^\prime } = {\left( {\frac{{{a^2}Kt}}{{aKt + 1}}} \right)^\prime } = \frac{{{a^2}K\left( {aKt + 1} \right) - {a^2}Kt.aK}}{{{{\left( {aKt + 1} \right)}^2}}} = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\)
b) Theo câu trên nếu \(x = \left[ C \right]\) thì \(x'\left( t \right) = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\)
Ta lại có \(K{\left( {a - x} \right)^2} = K{\left( {a - \frac{{{a^2}Kt}}{{aKt + 1}}} \right)^2} = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}}\) nên \(x'\left( t \right) = K{\left( {a - x} \right)^2}\)
c) Ta có \(\mathop {\lim }\limits_{x \to \infty } \left[ C \right] = \mathop {\lim }\limits_{x \to \infty } \left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}} = a\) (mol/l) nên nồng độ của chất \(C\) dần đến \(a\) (mol/l)
d) Ta có \(\mathop {\lim }\limits_{x \to \infty } x'\left( t \right) = \mathop {\lim }\limits_{x \to \infty } = \frac{{{a^2}K}}{{{{\left( {aKt + 1} \right)}^2}}} = 0\) (mol/l) nên tốc độ phản ứng dần đến \(0\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: \(P'\left( t \right) = \frac{{0,75a{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {b + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}},t \ge 0\).
Theo đề bài, ta có: \(P\left( 0 \right) = 20\) và \(P'\left( 0 \right) = 12\).
Do đó, ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\frac{a}{{b + 1}} = 20}\\{\frac{{0,75a}}{{{{\left( {b + 1} \right)}^2}}} = 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 20\left( {b + 1} \right)}\\{\frac{{15}}{{b + 1}} = 12.}\end{array}} \right.} \right.\)
Giải hệ phương trình này, ta được \(a = 25\) và \(b = \frac{1}{4}\).
Khi đó, \(P'\left( t \right) = \frac{{18,75{{\rm{e}}^{ - 0,75t}}}}{{{{\left( {\frac{1}{4} + {{\rm{e}}^{ - 0,75t}}} \right)}^2}}} > 0,\forall t \ge 0\), tức là số lượng quần thể nấm men luôn tăng.
Tuy nhiên, do \(\mathop {\lim }\limits_{t \to + \infty } P\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25}}{{\frac{1}{4} + {{\rm{e}}^{ - 0.75t}}}} = 100\) nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Xét hàm số \(y = C\left( x \right) = \frac{{300x}}{{100 - x}},0 \le x < 100\).
Ta có:\(y' = \frac{{30000}}{{{{\left( {100 - x} \right)}^2}}} > 0\), với mọi \(x \in [0;100)\). Do đó hàm số luôn đồng biến trên nửa khoảng \(\left[ {0;100} \right)\) và\(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {{100}^ - }} \frac{{300x}}{{100 - x}} = + \infty \) nên đồ thị hàm số có tiệm cận đứng là \(x = 100\).
Bảng biến thiên:
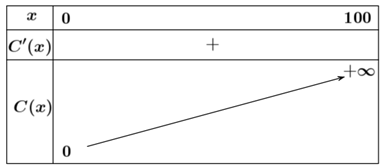
a) Chi phí cần bỏ ra \(C\left( x \right)\) sẽ luôn tăng khi \(x\) tăng.
b) Vì \(\mathop {\lim }\limits_{x \to {{100}^ - }} C\left( x \right) = + \infty \) (hàm số \(C\left( x \right)\) không xác định khi \(x = 100)\) nên nhà máy không thể loại bỏ \(100\% \) chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập